In a parallelogram ABCD, AB = 10 cm and AD = 6 cm. The bisector of ∠A meets DC in E. AE and BC produced meet at F. Find the length of CF.
To solve the problem step by step, we will analyze the given parallelogram ABCD with the given dimensions and the properties of angle bisectors and parallel lines.
1. Identify the Given Information:
- In parallelogram ABCD, we have:
- AB = 10 cm
- AD = 6 cm
2. Properties of Parallelograms:
- In a parallelogram, opposite sides are equal. Therefore:
- BC = AB = 10 cm
- CD = AD = 6 cm
3. Draw the Angle Bisector:
- The angle bisector of angle A meets side DC at point E.
4. Extend Lines:
- Extend lines AE and BC to meet at point F.
5. Construct Triangle AEF:
- In triangle AEF, since AE is the angle bisector, we can use the Angle Bisector Theorem which states that:
BEEC=ABAD
- Substituting the known values:
BEEC=106=53
6. Let EC = 3x and BE = 5x:
- From the angle bisector theorem, we can express BE and EC in terms of a variable x:
- BE = 5x
- EC = 3x
7. Calculate Length of DC:
- Since DC = BE + EC:
DC=5x+3x=8x
- We know that DC = 6 cm (as AD = 6 cm), therefore:
8x=6⟹x=68=34 cm
8. Find BE and EC:
- Now substituting x back to find BE and EC:
- BE = 5x = 5 \times \frac{3}{4} = \frac{15}{4} \text{ cm} = 3.75 \text{ cm}
- EC = 3x = 3 \times \frac{3}{4} = \frac{9}{4} \text{ cm} = 2.25 \text{ cm}
9. Determine Length CF:
- Since CF is the remaining part of DC after EC:
CF=DC−EC=6−EC=6−2.25=3.75 cm
Final Answer:
Thus, the length of CF is 3.75 cm.
- In parallelogram ABCD, we have:
- AB = 10 cm
- AD = 6 cm
- In a parallelogram, opposite sides are equal. Therefore:
- BC = AB = 10 cm
- CD = AD = 6 cm
- The angle bisector of angle A meets side DC at point E.
- Extend lines AE and BC to meet at point F.
- In triangle AEF, since AE is the angle bisector, we can use the Angle Bisector Theorem which states that:
BEEC=ABAD
- Substituting the known values:
BEEC=106=53
- From the angle bisector theorem, we can express BE and EC in terms of a variable x:
- BE = 5x
- EC = 3x
- Since DC = BE + EC:
DC=5x+3x=8x
- We know that DC = 6 cm (as AD = 6 cm), therefore:
8x=6⟹x=68=34 cm
- Now substituting x back to find BE and EC:
- BE = 5x = 5 \times \frac{3}{4} = \frac{15}{4} \text{ cm} = 3.75 \text{ cm}
- EC = 3x = 3 \times \frac{3}{4} = \frac{9}{4} \text{ cm} = 2.25 \text{ cm}
- Since CF is the remaining part of DC after EC:
CF=DC−EC=6−EC=6−2.25=3.75 cm
Thus, the length of CF is 3.75 cm.
Topper's Solved these Questions
Similar Questions
In a parallelogram ABCD, AB = 10 cm and AD = 6 cm. The bisector of ∠A meets DC in E. AE and BC produced meet at F. Find the length of CF.
View SolutionIn a parallelogram PQRS, PQ = 12 cm and PS = 9 cm. The bisector of ∠P meet SR in M. PM and QR both when produced meet at T. Find the length of RT.
View Solution
Knowledge Check
In a parallelogram ABCD, the bisector of anl≥A also bisects BC at E, find the AD.
AABB2ABC3ABD12ABA parallelogram ABCD has sides AB = 24 cm and AD = 16 cm. The distance between the sides AB and DC is 10 cm. Find the distance between the sides AD and BC.
A16 cmB18 cmC15 cmD26 cmIn a triangle ABC, AB = 5 cm, BC = 6 cm and CA = 7 cm. If bisectors of ∠A,∠B,∠C respectively meet sides BC, CA and AB at D. E, F and I be the incentre of the triangle then
What is the length of AE ?A4211 cmB6 cmC132 cmD3511 cm
In a ΔABC, AC = 12 cm, AB = 16 cm and AD is the bisector of ∠A. If BD = 4 cm, then what is DC equal to ?
View SolutionIn a parallelogram ABCD, the bisectors of ∠A and ∠B meet at O. Find ∠AOB.
View SolutionIn a triangle ABC, AB = 5 cm, BC = 6 cm and CA = 7 cm. If bisectors of ∠A,∠B,∠C respectively meet sides BC, CA and AB at D. E, F and I be the incentre of the triangle then
What is BD : DC ?
View SolutionABCD is a parallelogram and L is a point on DB . The produced line AL meets BC at M and DC produced at N .
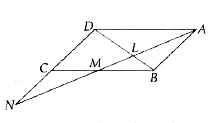
Given that DL =3LB , find ABCN .
View SolutionIn a ΔABC, AD is a median . The bisectors of ∠ADBand∠ADC meet AB and AC at E and F respectively . If the ratio of AE : BE =2:3 , then find the ratio of EF : BC.
View Solution
