In a right angle triangle ΔABC is which ∠B=90∘ a circle is drawn with AB diameter intersecting the hypotenuse AC at P.Prove that the tangent to the circle at PQ bisects BC.
Let O be the centre of the given circle. Suppose, the tangent at P meets BC at Q. Join BP.
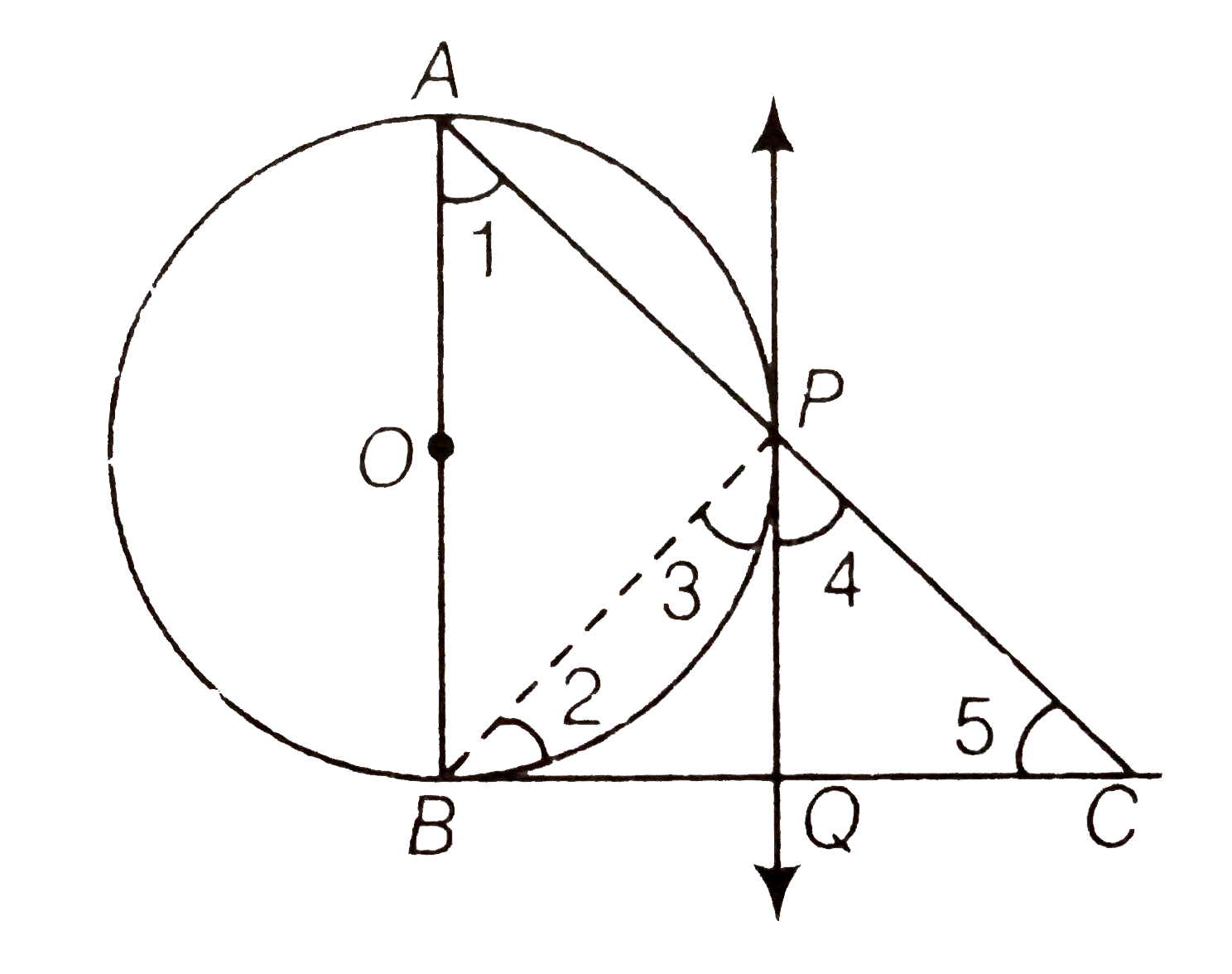
To prove BQ=QC [angles in alternate segment]
Proof ∠ABC=90∘
[tangent at any point of circle is perpendicular to radius through the point of contact] :.In ΔABC, ∠1+∠5=90∘ [angle sum property, [∠ABC=90∘]
∠3=∠1
[angle between tangent and the chord equals angle made by the chord in alternate segment]
∴∠3+∠5=90∘.....(i)
Also, ∴∠APB=90∘ [angle in semi-circle]
⇒∠3+∠4=90∘ [∠APB+∠BPC=180∘,linera pair]
From Eqs. (i) and (ii), we get
∠3+∠5+∠3+∠4
⇒∠5=∠4
⇒PQ=QC [sides opposite to equal angles are equal]
Also, QP=QB
[tangents drawn from an internal point to a circle are equal]
⇒QB=QC Hence proved.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - EXERCISE 9.3 SHORT ANSWER TYPE QUESTIONS10videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - Long Answer Type Questions10videos
ARITHMETIC PROGRESSIONS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Exercise 10.4 Long Answer type Questions7videos
CONSTRUCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
In right triangle, ABC, AB=10,BC=8,AC=6.
A35B34C45D54
Construct a right angled ΔABC in which BC=5cm,∠B=90∘andAB=4cm.
View SolutionIf a circle is inscribed in right angled triangle ABC with right angle at B, show that the diameter of the circle is equal to AB+BC−AC.
View SolutionConstruct a right angled ΔABC in which ∠B=90∘,BC=4cm and hypotenuse CA=5cm.
View SolutionABC is a right triagle with angle B=90∘ . A circle with BC as diameter meets hypotenuse AC and point D. Prove that
(i) AC×AD=AB2
(ii) BD2=AD×DCView SolutionProve that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base. Given: A △ABC in which AB=AC and a circle is drawn by taking AB as diameter which intersects the side BC of triangle at D. To Prove: BD=DC Construction : Join AD.
View SolutionConstruct a right triangle ABC in which ∠B=90∘,BC=3.6cmandCA=5.4cm,
View SolutionΔABC is a right triangle right angled at A such that AB=AC and bisector of ∠C intersects the side AB at D. Prove that AC+AD=BC.
View Solution

