In a school there are two sections section A and section B of class X . There are 32 students in section A and 36 students in section B . Determine the minimum number of books required for their class library so that they can be distributed equally among students of section A or section B .
To determine the minimum number of books required for the class library so that they can be distributed equally among students of section A or section B, we need to find the least common multiple (LCM) of the number of students in each section.
1. Identify the number of students in each section:
- Section A has 32 students.
- Section B has 36 students.
2. Find the prime factorization of each number:
- For 32:
- 32 can be expressed as 25 (since 32=2×2×2×2×2).
- For 36:
- 36 can be expressed as 22×32 (since 36=2×2×3×3).
3. Determine the highest power of each prime factor:
- The prime factors involved are 2 and 3.
- The highest power of 2 from both factorizations is 25 (from 32).
- The highest power of 3 is 32 (from 36).
4. Calculate the LCM using the highest powers:
- LCM = 25×32
- Calculate 25=32 and 32=9.
- Now, multiply these results:
LCM=32×9=288
5. Conclusion:
- The minimum number of books required for their class library, so that they can be distributed equally among students of section A or section B, is 288.
- Section A has 32 students.
- Section B has 36 students.
- For 32:
- 32 can be expressed as 25 (since 32=2×2×2×2×2).
- For 36:
- 36 can be expressed as 22×32 (since 36=2×2×3×3).
- The prime factors involved are 2 and 3.
- The highest power of 2 from both factorizations is 25 (from 32).
- The highest power of 3 is 32 (from 36).
- LCM = 25×32
- Calculate 25=32 and 32=9.
- Now, multiply these results:
LCM=32×9=288
- The minimum number of books required for their class library, so that they can be distributed equally among students of section A or section B, is 288.
Topper's Solved these Questions
Similar Questions
In a school there are two sections - section A and section B of Class VI. There are 32 students in section A and 36 in section B. Determine the minimum number of books required for their class library so that they can be distributed equally among students of section A or section B.
View SolutionIn a school there are five sections of class IX. The number of students in each section is given below.
Construct a bar graph.

View SolutionIn a school, there are five sections of class IX. The number of students in each section is given below. Construct a bar graph representing this data: Section: A B C D E No. of Students 40 48 52 45 30
View SolutionThere are 100 students in class VII in a school. 40 students are in Section A, 33 in Section B, and the remaining students are in Section C. Find what percentage of students are there in each section.
View SolutionIn a school, there are five sections of class VII. The number of students in each section is given below. Construct a bar graph representing this data: Section, A, B, C, D, E No. of Students, 40, 48, 52, 45, 30
View SolutionThe number of students in section X A and X B are 30 and 35 respectively. The mean scores of students in the mathematices test are as follows:

View SolutionIn a particular section of class IX, 40 students were asked about the month of their birth and the following graph was prepared for the data so obtained.

Find the probability that a student of the class was born in August.
View SolutionThe potential difference between points A and B, in a section of a circuit shown in
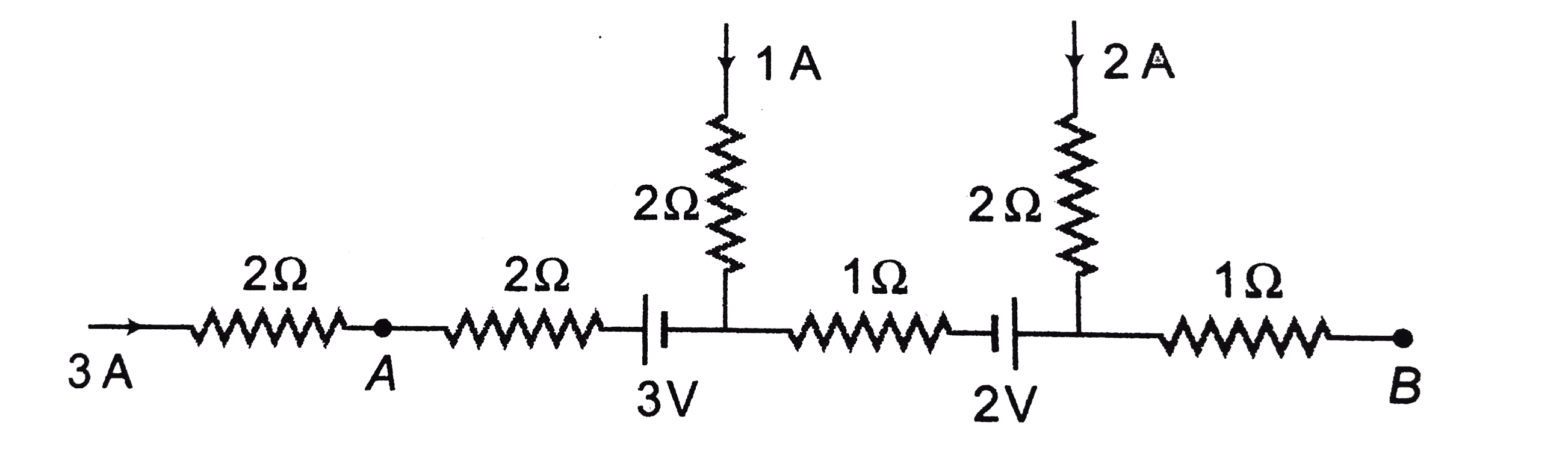
View SolutionThere are three sections in a question paper, each containing 5 questions. A candidate has to solve any 5 questions, choosing at least one from each section. Find the number of ways in which the candidate can choose the questions.
View SolutionLet there are 4 sections of 25 students each in a coaching class. Now, out of 150 students 100 are to be selected randomly and enrolled in these sections. Then, the probability that the students A and B (both present in 150 students) are selected and placed in the same section, is
View Solution
