In a triangle ABC, E is the mid-point of median AD. Show that ar(△BED)=14ar(△ABC).
To solve the problem, we need to show that the area of triangle BED is equal to 14 times the area of triangle ABC. Let's go through the solution step by step.
Step 1: Understand the Given Information
In triangle ABC, E is the midpoint of median AD. By definition, a median divides the opposite side into two equal parts. Therefore, D is the midpoint of side BC.
Step 2: Area of Triangle ABC
The area of triangle ABC can be calculated using the formula:
Area of △ABC=12×Base×Height
Here, we can take BC as the base and AD as the height from point A to line BC. Therefore:
Area of △ABC=12×BC×AD
Let’s denote this as Equation (1).
Step 3: Area of Triangle BED
Next, we need to find the area of triangle BED. The base of triangle BED is BD, and the height is DE. Since D is the midpoint of BC, we have:
BD=12×BC
Since E is the midpoint of AD, we have:
DE=12×AD
Now, we can calculate the area of triangle BED:
Area of △BED=12×Base×Height=12×BD×DE
Substituting the values of BD and DE:
Area of △BED=12×(12×BC)×(12×AD)
This simplifies to:
Area of △BED=12×12×12×BC×AD=18×BC×AD
Let’s denote this as Equation (2).
Step 4: Relate the Areas
Now, we can relate the areas of triangle ABC and triangle BED using Equations (1) and (2):
From Equation (1):
Area of △ABC=12×BC×AD
From Equation (2):
Area of △BED=18×BC×AD
Step 5: Finding the Ratio of the Areas
Now, we find the ratio of the areas:
Area of △ABCArea of △BED=12×BC×AD18×BC×AD
The BC and AD terms cancel out:
Area of △ABCArea of △BED=1/21/8=1/2×8/1=4
Thus, we have:
Area of △ABC=4×Area of △BED
This implies:
Area of △BED=14×Area of △ABC
Conclusion
We have shown that:
Area of △BED=14×Area of △ABC
Hence, the proof is complete.
In triangle ABC, E is the midpoint of median AD. By definition, a median divides the opposite side into two equal parts. Therefore, D is the midpoint of side BC.
The area of triangle ABC can be calculated using the formula:
Area of △ABC=12×Base×Height
Here, we can take BC as the base and AD as the height from point A to line BC. Therefore:
Area of △ABC=12×BC×AD
Let’s denote this as Equation (1).
Next, we need to find the area of triangle BED. The base of triangle BED is BD, and the height is DE. Since D is the midpoint of BC, we have:
BD=12×BC
Since E is the midpoint of AD, we have:
DE=12×AD
Now, we can calculate the area of triangle BED:
Area of △BED=12×Base×Height=12×BD×DE
Substituting the values of BD and DE:
Area of △BED=12×(12×BC)×(12×AD)
This simplifies to:
Area of △BED=12×12×12×BC×AD=18×BC×AD
Let’s denote this as Equation (2).
Now, we can relate the areas of triangle ABC and triangle BED using Equations (1) and (2):
From Equation (1):
Area of △ABC=12×BC×AD
From Equation (2):
Area of △BED=18×BC×AD
Now, we find the ratio of the areas:
Area of △ABCArea of △BED=12×BC×AD18×BC×AD
The BC and AD terms cancel out:
Area of △ABCArea of △BED=1/21/8=1/2×8/1=4
Thus, we have:
Area of △ABC=4×Area of △BED
This implies:
Area of △BED=14×Area of △ABC
We have shown that:
Area of △BED=14×Area of △ABC
Hence, the proof is complete.
Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - NCERT SECTION ( EXERCISE 9.4)
19 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE ( Multiple Choice Questions )
45 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - NCERT SECTION ( EXERCISE 9.2)
7 Videos
- CIRCLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - OLYMPIAD/HOTS CORNER
6 Videos
Similar Questions
Knowledge Check
In △ABC, if D is the midpoint of BC and E is the midpoint of AD then ar(△BED) = ?
 A12ar(△ABC)B13ar(△ABC)C14ar(△ABC)D23ar(△ABC)
A12ar(△ABC)B13ar(△ABC)C14ar(△ABC)D23ar(△ABC)
ABC is a triangle in which D is the midpoint of BC and E is the midpoint of AD.
Prove that ar(△BED)=14ar(△ABC).

View SolutionIn the figure, E is any point on median AD of a △ABC. Show that ar(△ABE)= ar(△ACE).
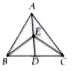
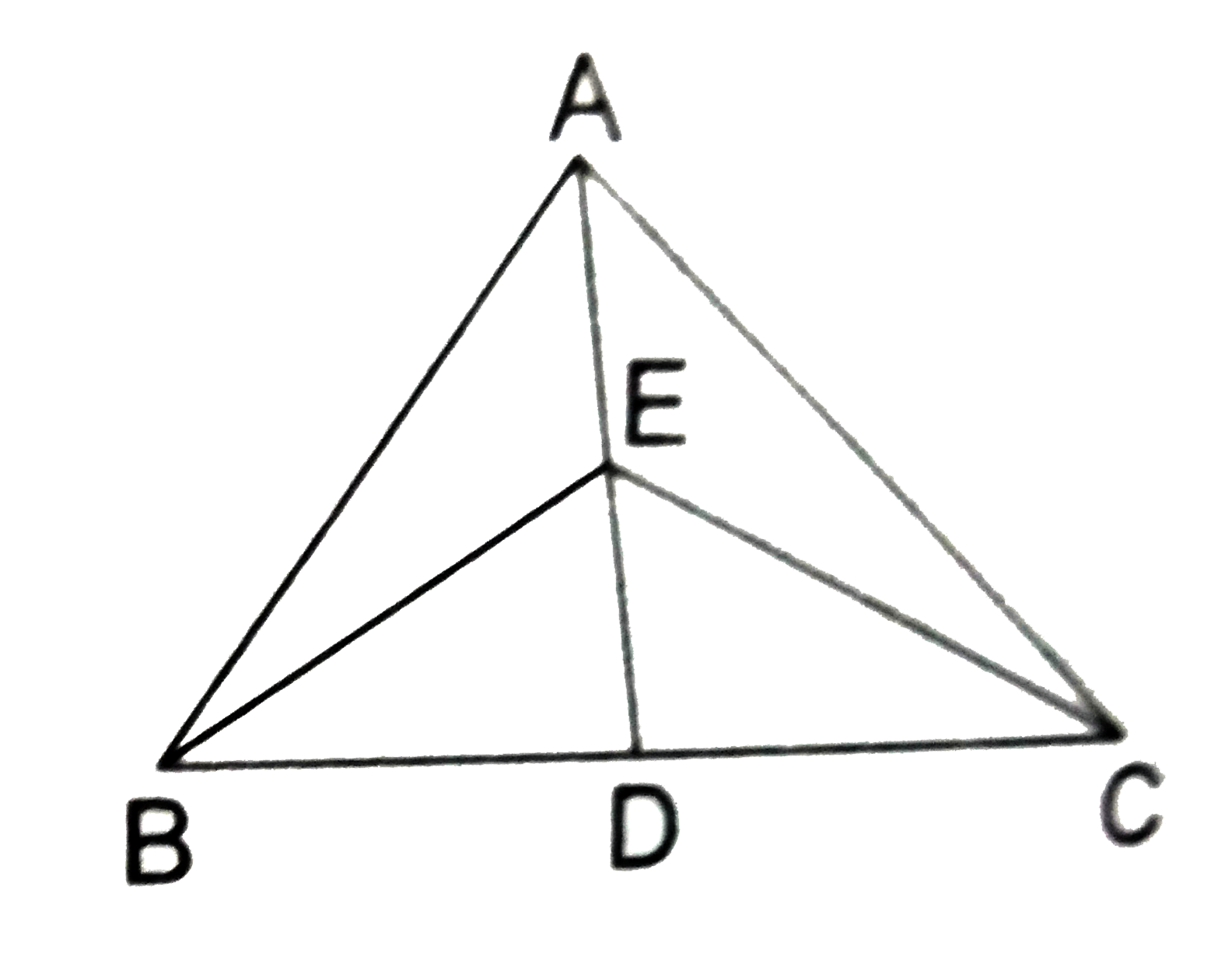
View SolutionThe vertex A of △ABC is joined to a point D on the side BC. The midpoint of AD is E.
Prove that ar(△BEC)=12ar(△ABC).
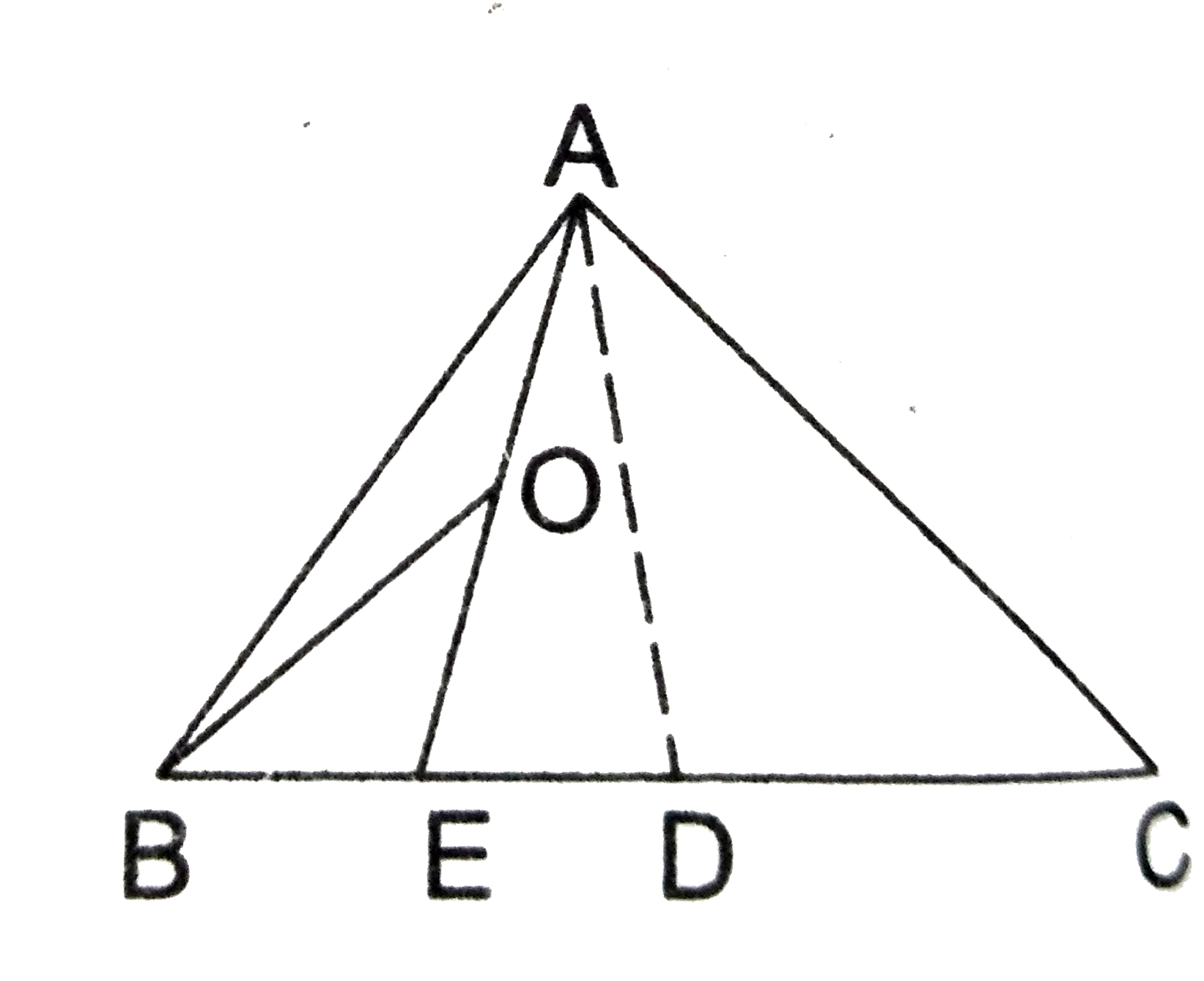
View SolutionD is the midpoint of side BC of △ABC and E is the midpoint of BD. If O is the midpoint of AE,
prove that ar(△BOE)=18ar(△ABC).
View SolutionP and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show that
ar(ΔPRQ) = 1/2 ar(ΔARC)
View SolutionE is any point on median AD of AABC If ar(△ABE) = 10 cm thenar(△ACE) is
View SolutionD, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that
ar(△DEF)=14ar(△ABC)
View Solution
