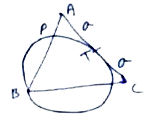
In ΔABC,AB=AC. A circle passing through B touches side AC at its midpoint P and intersects side AB at Q then prove BQ = 3AQ
Construction : Draw seg BP and seg PQ
In ΔAPQ and ΔABP,
∠APQ≅∠ABP …(Tangent secant theorem )
∠PAQ≅∠BAP …(Common angle )
∴ΔAPQ~ΔABP …(AA test of similarity )
∴APAB=AQAP ….(c.s.s.t.)
∴12ACAB=AQ12AC= ...(∵ P is the midpoint of seg AC )
∴12ABAB=AQ12AB ...(∴AB=AC)
∴AQ=12×12AB
∴AQ=14AB
∴AB=4AQ
BQ+AQ=AB ...(A-Q-B)<br>BQ + AQ = 4AQ <br>:. BQ = 4AQ - AQ <br>:. BQ = 3AQ
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - ASSIGNMENT 4.110videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - ASSIGNMENT 4.26videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - 4.4 (1 mark each)9videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :1videos
CHALLENGING QUESTIONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - COORDINATE GEOMETRY EXERCISE - Assignment 6.513videos
COORDINATE GEOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
ABC is an isosceles triangle with AB = AC. A circle through B touching AC at the middle point intersects AB at P. Then, AP : AB is
A3:5B1:4C4:1D2:3 - Question 2 - Select One
ABC is an isosceles triangle with AB = AC. A circle through B touching AC at the middle point intersects AB at P. Then AP : AB is :
A4:1B2:3C3:5D1:4 - Question 3 - Select One
ABC is an isosceles triangle with AB = AC. A circle through B touching AC at the middle point Intersects AB at P. Then AP: AB is :
A4:1B2:3C3:5D1:4

If a circle touches the side BC at point P, extended side AB at Q and extended side AC at R. Then AQ is equal to :View SolutionIn an isosceles triangle ABC with AB=AC, a circle passing through B and C intersects the sides AB and AC at D and E respectively. Prove that DEBC
View SolutionIn an isosceles triangle ABC with AB=AC, a circle passing through B and C intersects the sides ABandAC atDandE respectively. Prove that DECB.
View SolutionΔABC is a right triangle right angled at A such that AB=AC and bisector of ∠C intersects the side AB at D. Prove that AC+AD=BC.
View SolutionIn the figure, ABC is a triangle in which AB=AC. A circle through B touches AC at D and intersects AB at P. If D is the mid - point of AC, Find the value of AB :
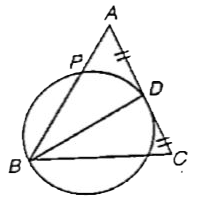 View Solution
View Solution