ΔABC is inscribed in a circle with centre O and line AP is a tangent at the point A. Ray AF is the bisector of ∠BAC
Prove that seg AP≅ seg PE.
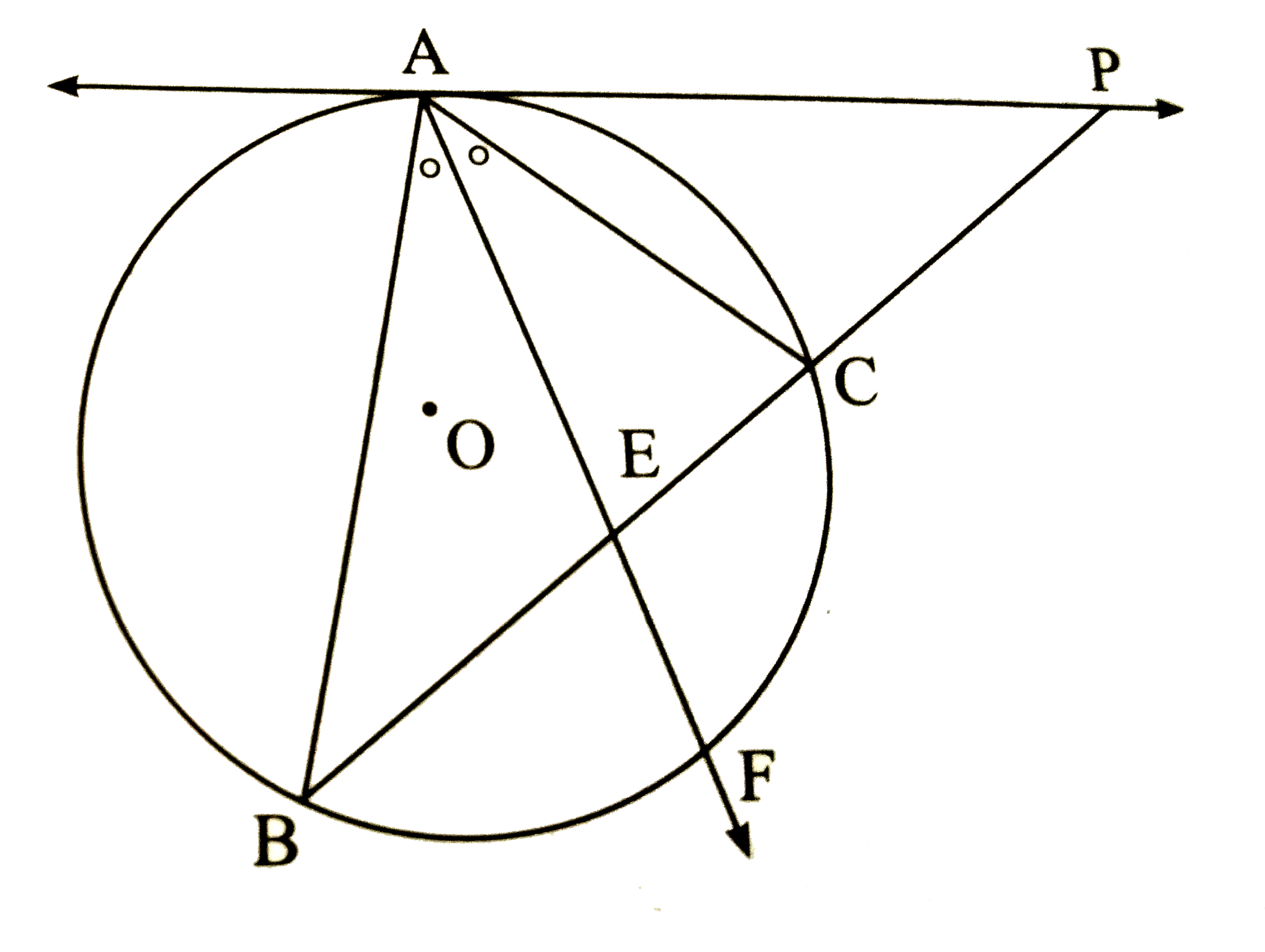
Line AP is a tangent and seg AC is a chord.
∴∠PAC=∠ABP …..(Angles in alternate segmets ) …(1)
∠PAE=∠PAC+∠CAE …(Angle addition postulate) …(2)
Ray AF is the bisector of ∠BAC …..(Given ) ….(3)
From (1), (2) and (3) ,
∠PAE=∠ABP+12∠BAC ....(4)
∠AEP=∠BAE+_ABP ...(Ray AF is the bisector of ∠BAC) ...(6)
From ( 4) and (6) ,
∠PAE=∠AEP
∴seg PA = seg PE ...(Sides opposite to equal angles in a triangle )
i.e., seg PA ≅ seg PE.
Topper's Solved these Questions
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - ASSIGNMENT 4.1
10 Videos
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - ASSIGNMENT 4.2
6 Videos
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - 4.4 (1 mark each)
9 Videos
- CHALLENGING QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :
1 Video
- COORDINATE GEOMETRY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - COORDINATE GEOMETRY EXERCISE - Assignment 6.5
13 Videos
Similar Questions
Solve any two of the following subquestions :
In the figure , O is the centre of the circles and AP is the tangent to the circle at point A . Ray AF is the bisector of ∠BAC
Prove : seg AP≅ seg PE<br>
View SolutionIf two chords AB and AC of a circle with centre O are such that the centre O lies on the bisector of ∠BAC; Prove that AB=AC
View Solution
Knowledge Check
If an equilateral triangle ABC is inscribed in a circle with centre O then the measure of ∠AOB is
A60∘B90∘C120∘D180∘Equilateral Δ ABC is inscribed in a circle with centre P. Then, ∠BPC = ..........
A60∘B90∘C120∘D75∘
AP is tangent to circle O at point P, What is the length of OP?
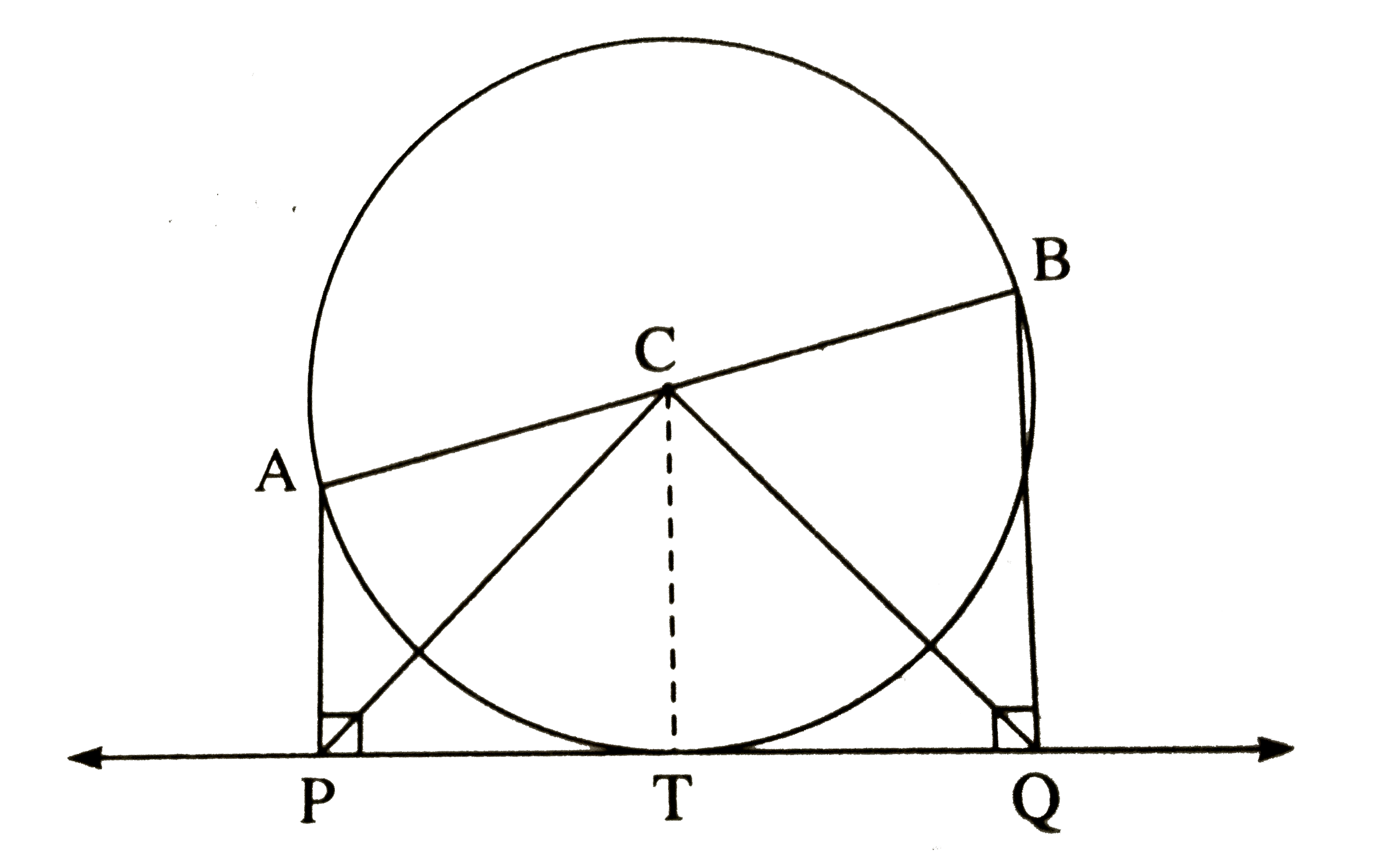
View SolutionIn the figure, seg AB is a diameter of a circle with centre C. Line PQ is a tangent , which touches the circle at point T. seg AP⊥ line PQ and seg BQ⊥ line PQ.
Prove that, seg CP≅ seg CQ.

View SolutionIf two chords AB and AC of a circle with centre O are such that the centre O lies on the bisector of ∠BAC, prove that AB=AC , i.e. the chords are equal.
View SolutionIn the figure, seg AB is a diameter of a circle with centre C. Line PQ is a tangent, which touches the circle at point T. seg AP ⊥ line PQ and seg BQ ⊥ line PQ. Prove that, seg CP ≅ seg CQ.
View SolutionTwo chord AB and AC of a circle are equal. Prove that the centre of a circle lies on the angle bisector of ∠BAC
View SolutionIn Figure, BC is a tangent to the circle with centre O.OE bisects AP. Prove that AEO~ABC.
View Solution