Let M be a point of contact of two internally touching circles. Let line AMB be their common tangent. The chord CD of the bigger circle touches the smaller circle at the point N. Chord CM and chord DM of the bigger circler intersect the smaller circle at the points P and R respectively.
Prove that ∠CMN≅∠DMN.
Construction : Draw seg NR.
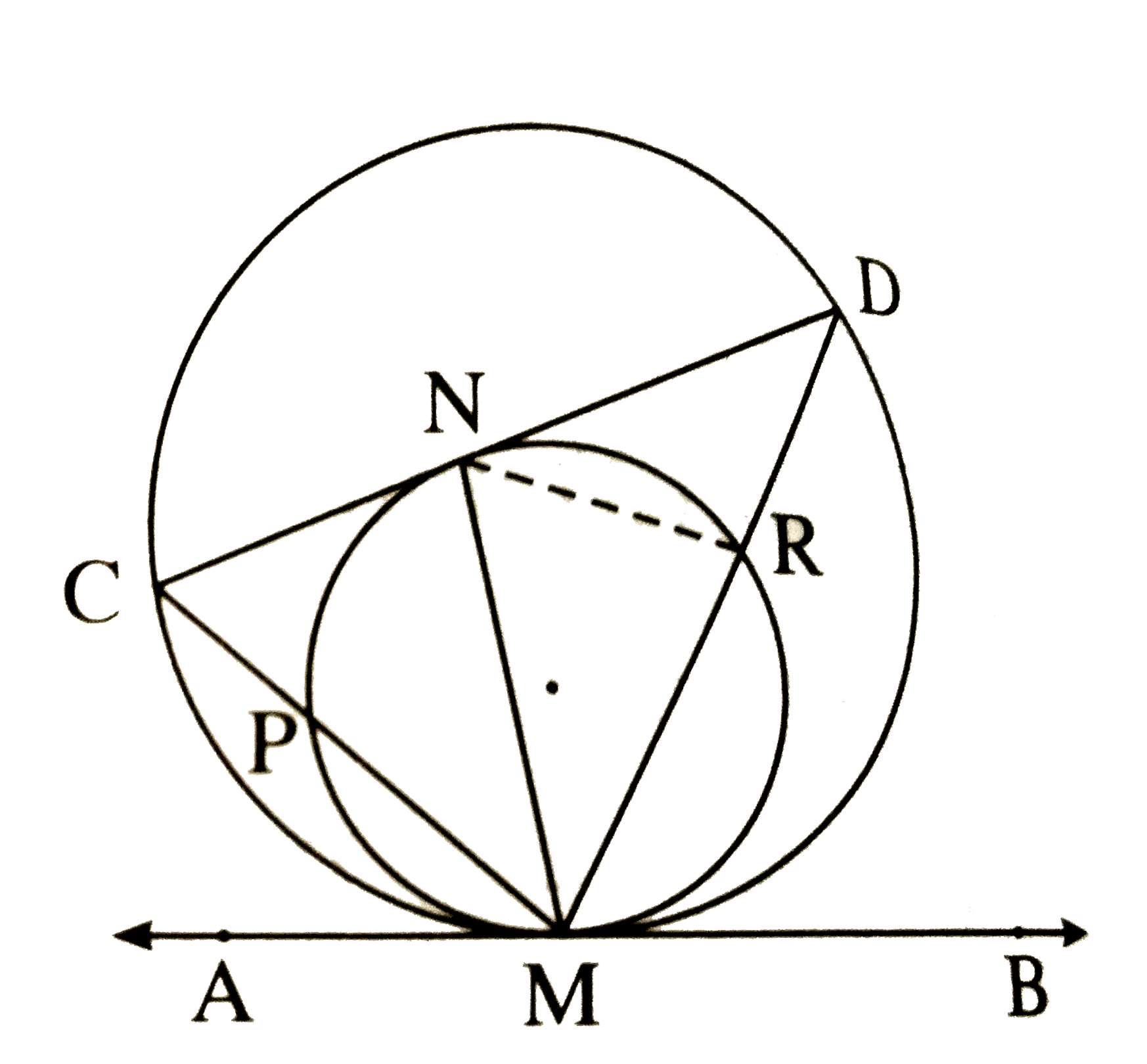
CD si a tangent to the smaller circle at the point N and NR is a chord of the smaller circle.
∴∠DNR≅∠NMR …(Tangent secant theorem ) …(1)
AB is a tangent to the lager circle at the point M and CM is th echord of the larger circle.
∴∠CMA≅∠CDM ...(Tangent secant theorem )
i.e., ∠CMA≅∠D ...(2)
AB is a tangent to the smaller circle at the point M and NM is a chord of the smaller circle .
∴∠NMA≅∠NRM ....(Tangent secant theorem ) ...(3)
For ΔNDR,∠NRM is the exterior theorem,
∠NRM=∠D+∠DNR ...(4)
∴∠NMA=∠CMA+∠NMR ........[From (3), (2) and (1) ] ....(5)
∠NMA=∠NMC+∠CMA ....(Angle addition postulate ) ...(6)
From (5) and (6)
∠NMC=∠NMR
∴∠NMC=∠NMD ...( ∠NMR is the same as ∠NMD)
i.e., ∠CMN≅∠DMN.
Topper's Solved these Questions
- CIRCLEBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:CIRCLEExercise:ASSIGNMENT 4.1
Explore 10 Videos
- CIRCLEBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:CIRCLEExercise:ASSIGNMENT 4.2
Explore 6 Videos
- CIRCLEBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:CIRCLEExercise:4.4 (1 mark each)
Explore 9 Videos
- CHALLENGING QUESTIONSBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:CHALLENGING QUESTIONSExercise:SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :
Explore 1 Video
- COORDINATE GEOMETRY Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:COORDINATE GEOMETRY Exercise:Assignment 6.5
Explore 13 Videos
Similar Questions
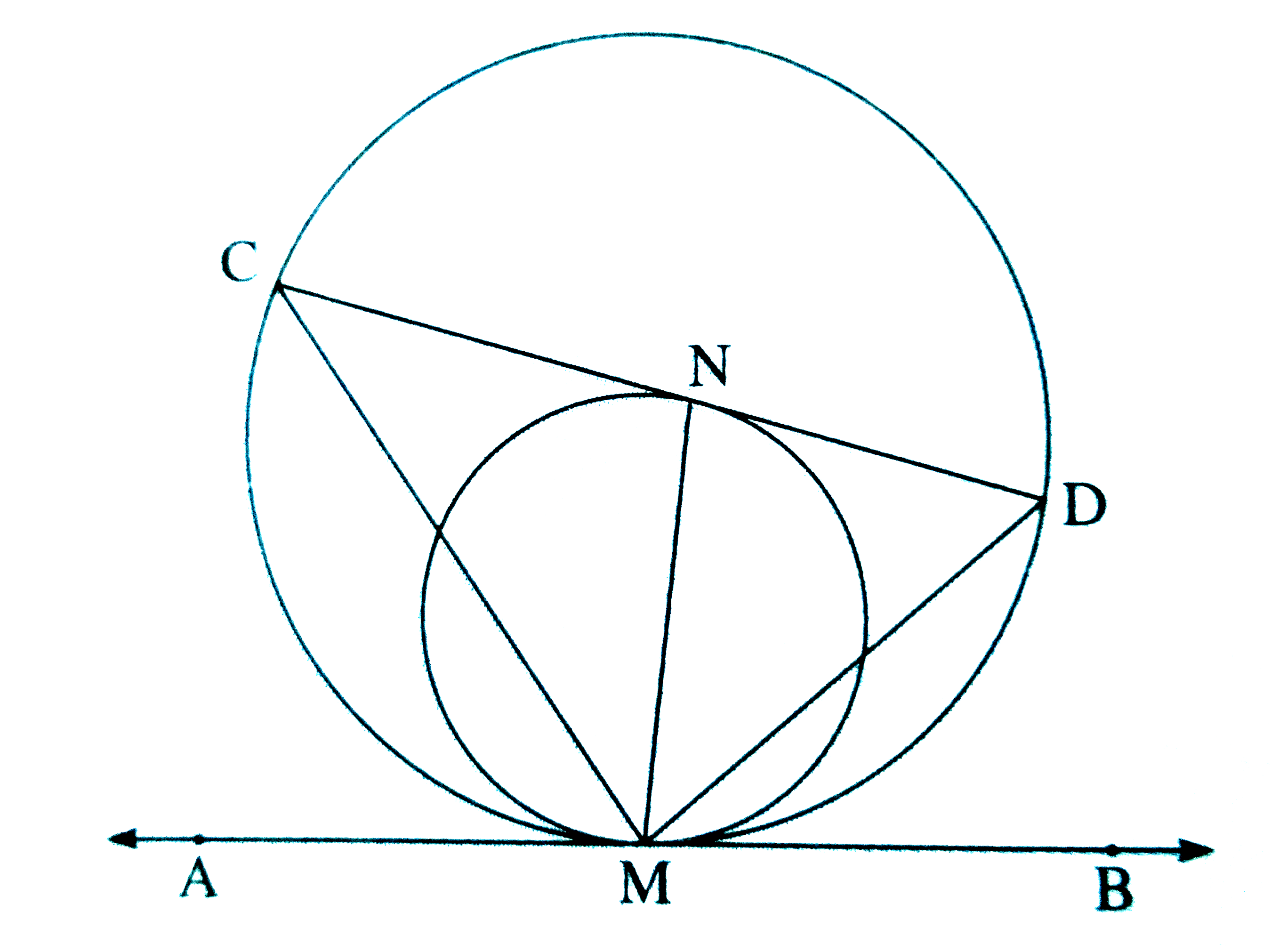
In the figure, M is the point of contact of two internally touching circles. The chord CD of the bigger circle touches the smaller circle at point N. Line AMB is their common tangent. Prove MN bisects ∠CMD
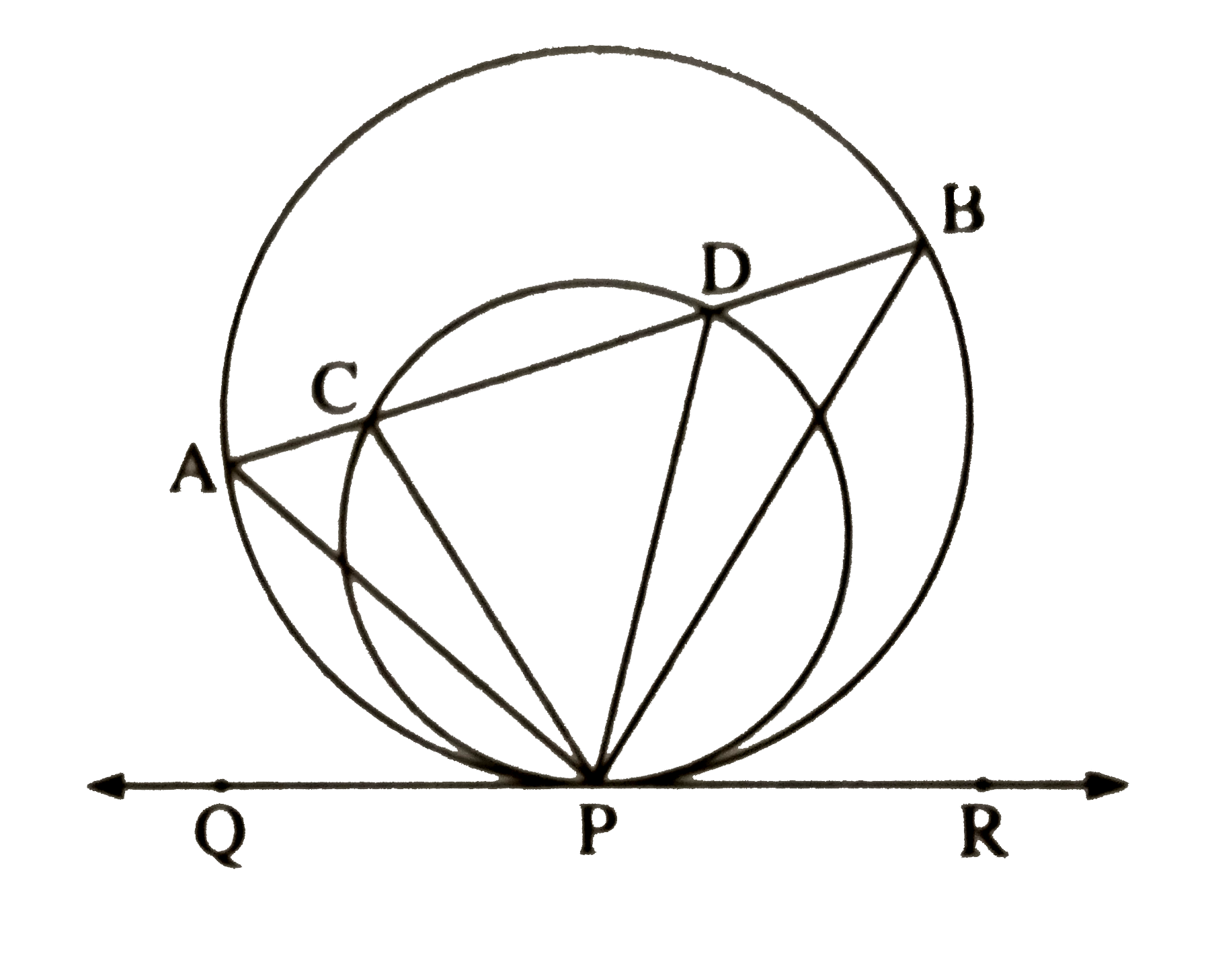
View SolutionIn the figure, two circles touch internally at point P. chord AB of the larger circle intersects the smaller circle in C and D. Prove ∠CPA≅∠DPB.
View Solution
Knowledge Check
Two concentric circles are of radii 13 cm and 5 cm. The length of the chord of the larger circle which touches the smaller circle is:
दो संकेंद्री वृत्तों की त्रिज्या 13 सेमी तथा 5 सेमी है। बड़े वृत्त की जीवा की लंबाई ज्ञात कीजिए, जो छोटे वृत्त को स्पर्श करती है।A6 cmB7 cmC10 cmD8 cmLet two chords AB and AC of the larger circle having same centre touch the smaller circle having same centre at X and Y. Then XY = ?
ABCB12BCC13BCD14BC
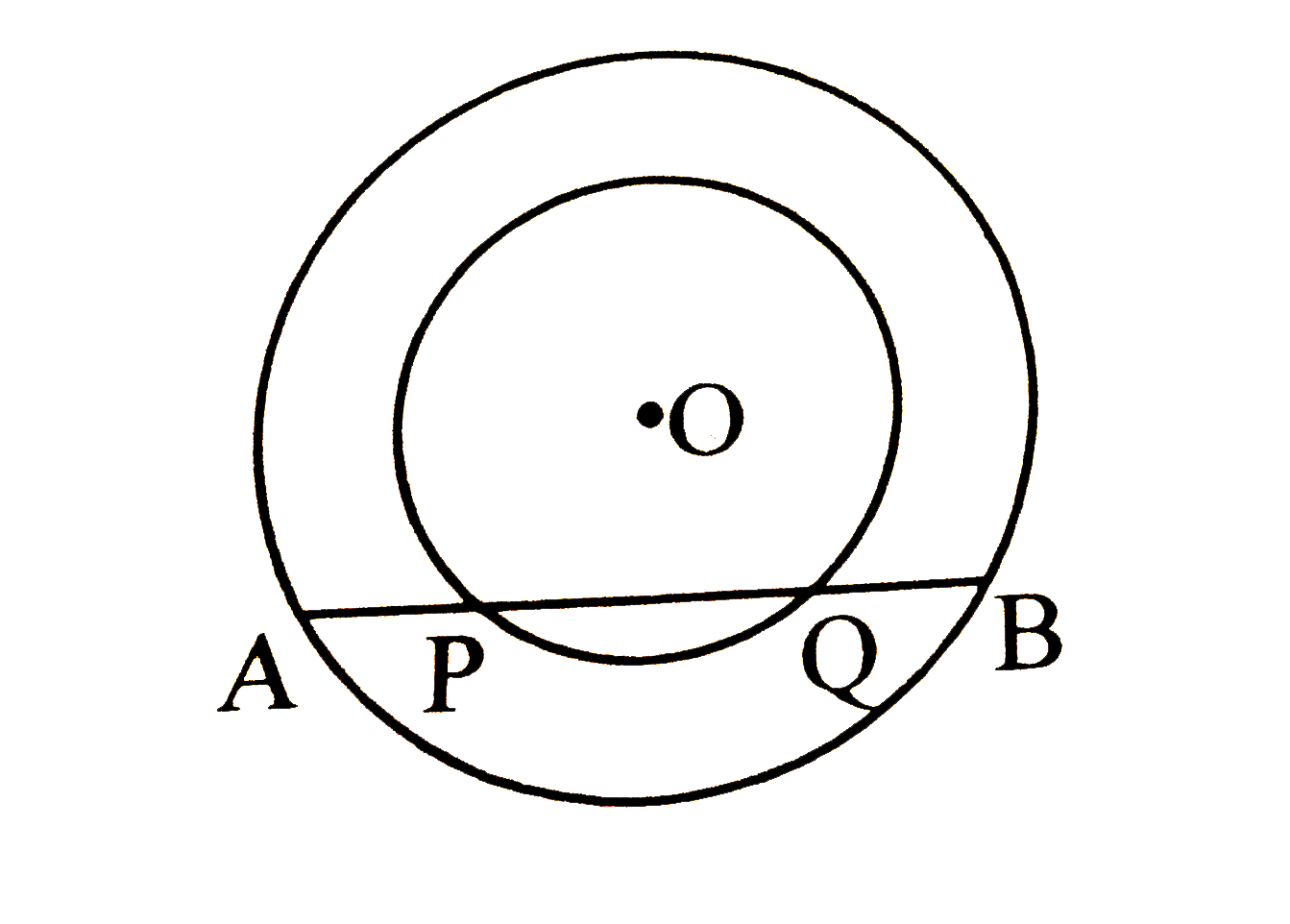
In the given figure, centre of two circles is O. Chord AB of bigger circle intersects the smaller circle in points P and Q . Show that AP = BQ.
View SolutionTwo concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
View SolutionTwo concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
View SolutionTwo concentric circles are of diameters 30cm and 18cm. Find the length of the chord of the larger circle which touches the smaller circle.
View SolutionTwo concentric circles are of diameter 30 cm and 18 cm. Find the length of the chord of the larger circle which touches the smaller circle.
View SolutionIn two concentric circles, a chord of length 8cm of the larger circle touches the smaller circle. If the radius of the larger circle is 5cm then find the radius of the smaller circle.
View Solution
