Question

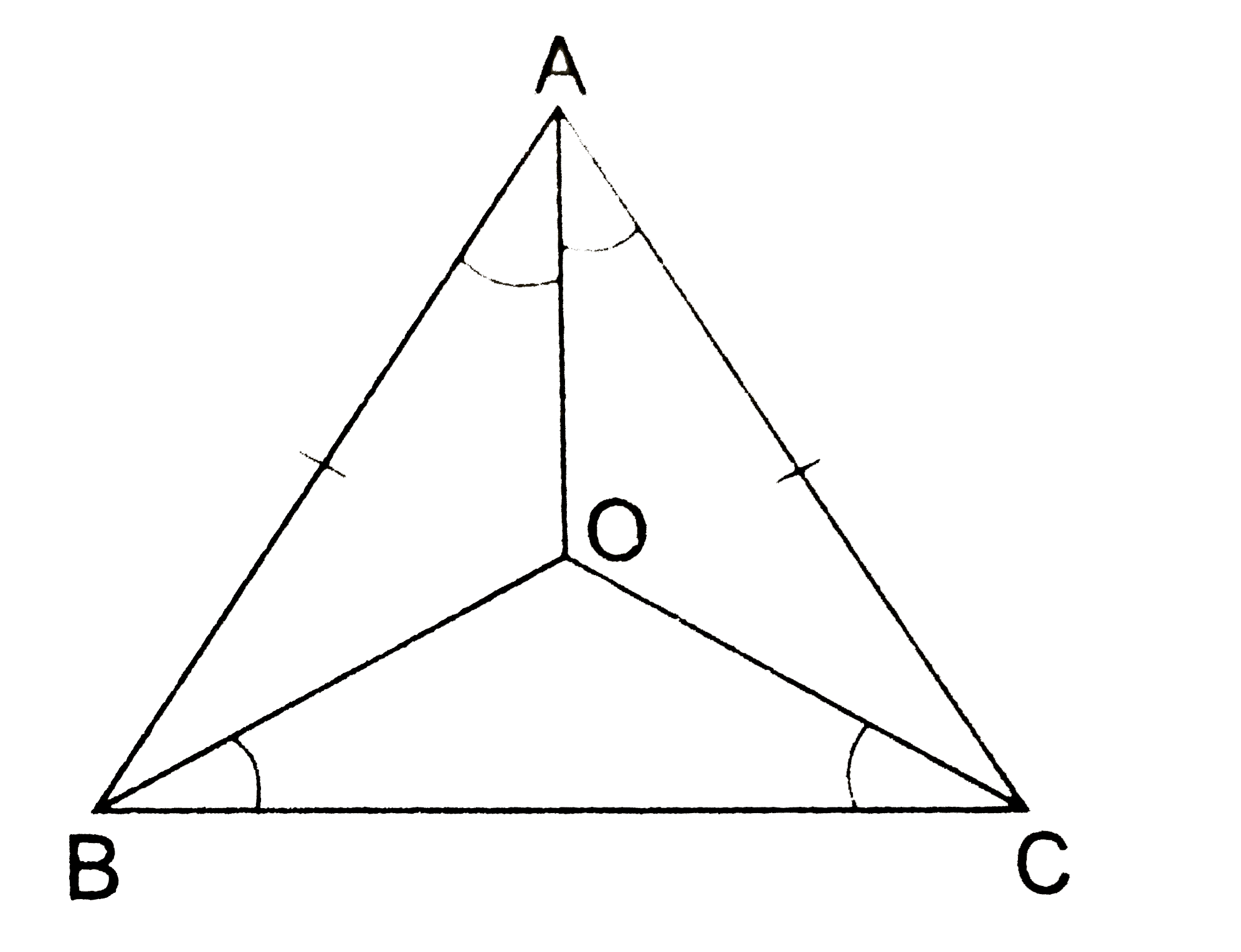
In $\Delta ABC,AB=AC$ and the bisectors of $\angle B$ and $\angle C$ meet AC and AB at point D and E respectively. Prove that $BD=CE$.

Explanation

To prove that $$BD=CE$$ in triangle $$\Delta ABC$$ where $$AB=AC$$ and the angle bisectors of $$\angle B$$ and $$\angle C$$ meet $$AC$$ and $$AB$$ at points $$D$$ and $$E$$ respectively, we can follow these steps:

1. Identify the Triangle and Given Information:
We have triangle \( \Delta ABC \) with \( AB = AC \). This means that triangle \( ABC \) is isosceles with \( \angle B = \angle C \).

Hint: Remember that in an isosceles triangle, the angles opposite the equal sides are also equal.

2. Draw the Angle Bisectors:
Draw the angle bisectors of \( \angle B \) and \( \angle C \). Let the angle bisector of \( \angle B \) intersect \( AC \) at point \( D \) and the angle bisector of \( \angle C \) intersect \( AB \) at point \( E \).

Hint: The angle bisector divides the angle into two equal parts.

3. Label the Angles:
Let \( \angle ABD = \angle DBC = \frac{1}{2} \angle B \) and \( \angle ACE = \angle ECA = \frac{1}{2} \angle C \).

Hint: Use the property of angle bisectors to express the angles in terms of \( \angle B \) and \( \angle C \).

4. Use the Isosceles Triangle Property:
Since \( AB = AC \), we have \( \angle B = \angle C \). Therefore, \( \frac{1}{2} \angle B = \frac{1}{2} \angle C \).

Hint: This equality allows us to establish relationships between the segments created by the angle bisectors.

5. Consider Triangles \( \Delta OBE \) and \( \Delta OCD \):
Let \( O \) be the intersection of \( BD \) and \( CE \). In triangles \( \Delta OBE \) and \( \Delta OCD \), we have:
- \( \angle OBE = \frac{1}{2} \angle B \)
- \( \angle OCD = \frac{1}{2} \angle C \)

Since \( \angle B = \angle C \), we can say \( \angle OBE = \angle OCD \).

Hint: Use the property of equal angles to establish similarity between the triangles.

6. Establish Similarity:
Since \( \angle OBE = \angle OCD \) and \( \angle OEB = \angle ODC \) (both are vertical angles), triangles \( \Delta OBE \) and \( \Delta OCD \) are similar by AA (Angle-Angle) similarity criterion.

Hint: Similar triangles have proportional sides.

7. Set Up Proportions:
From the similarity of triangles \( OBE \) and \( OCD \), we have:
\( \frac{OE}{OB} = \frac{OD}{OC} \)

Hint: Write down the ratios of corresponding sides from the similar triangles.

8. Express \( BD \) and \( CE \):
Since \( BD = OB + OD \) and \( CE = OC + OE \), we can express these segments in terms of the segments we have established.

Hint: Use the relationships from the previous steps to express \( BD \) and \( CE \).

9. Conclude that \( BD = CE \):
By substituting the expressions from the similarity into \( BD \) and \( CE \), we find that \( BD = CE \).

Hint: Combine the results to show that both segments are indeed equal.

Final Statement:
Thus, we have proved that \( BD = CE \).