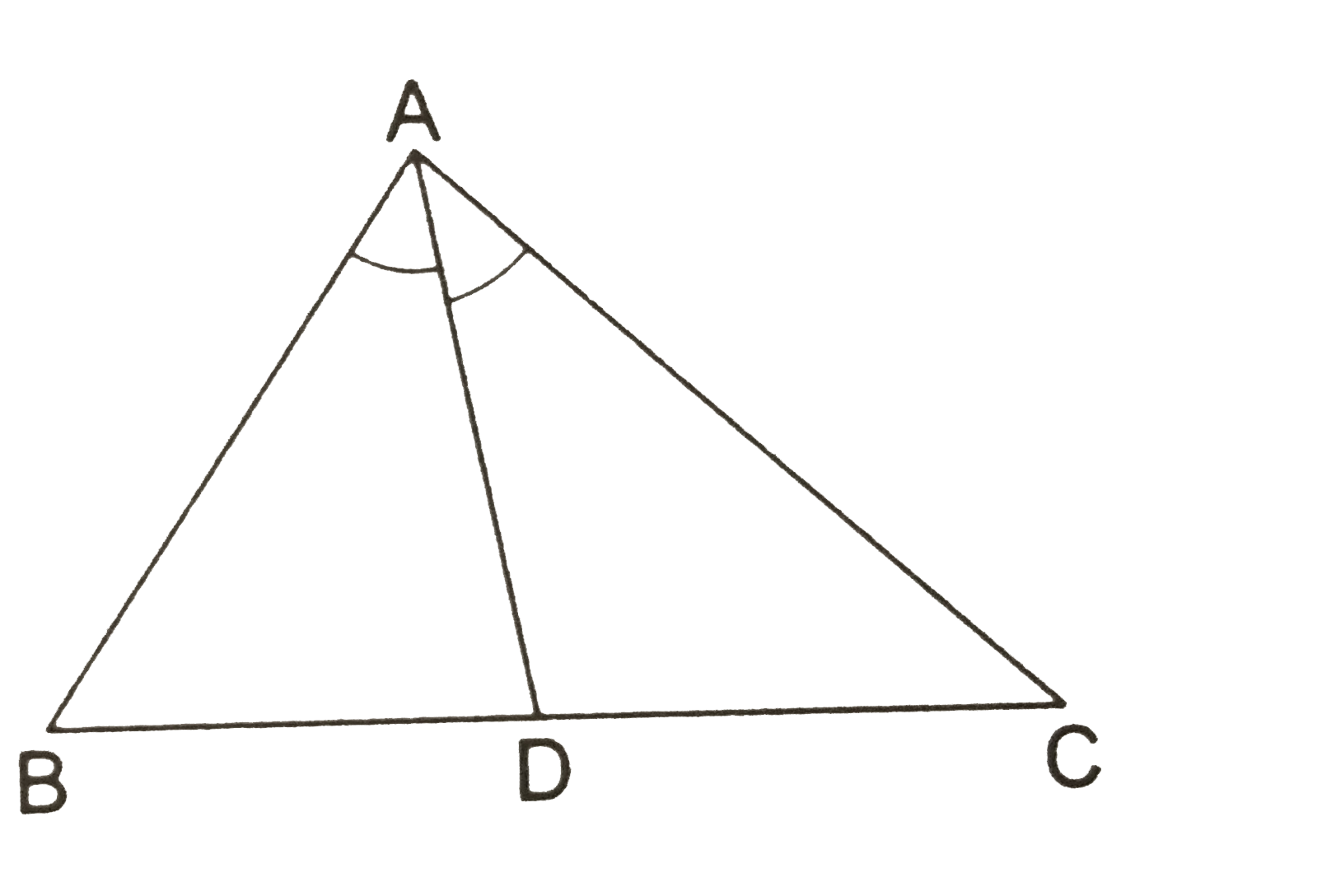
In ΔABC,AD is the bisector of ∠A . Then , ar(ΔABD)ar(ΔACD)=
AB2AC2
ABAC
BMCM
None of these
The correct Answer is:B
To find the ratio of the areas of triangles ABD and ACD in triangle ABC, where AD is the angle bisector of angle A, we can follow these steps:
1. Understanding the Problem: We have triangle ABC with AD as the angle bisector of angle A. We need to find the ratio of the areas of triangles ABD and ACD.
2. Using the Angle Bisector Theorem: According to the angle bisector theorem, the ratio of the lengths of the two segments created by the angle bisector on the opposite side is equal to the ratio of the other two sides of the triangle. Therefore, we have:
ABAC=BDDC
3. Area of Triangle Formula: The area of a triangle can be calculated using the formula:
Area=12×base×height
For triangle ABD, the base is BD and the height is the perpendicular dropped from A to line BD. For triangle ACD, the base is DC and the height is the same perpendicular from A.
4. Calculating Areas:
- Area of triangle ABD:
AreaABD=12×BD×h
- Area of triangle ACD:
AreaACD=12×DC×h
5. Finding the Ratio of Areas:
Now we can find the ratio of the areas of triangles ABD and ACD:
AreaABDAreaACD=12×BD×h12×DC×h
Here, the 12 and h cancel out:
AreaABDAreaACD=BDDC
6. Substituting from the Angle Bisector Theorem:
From the angle bisector theorem, we know that:
BDDC=ABAC
Therefore, we can conclude:
AreaABDAreaACD=ABAC
Final Result:
AreaABDAreaACD=ABAC
ABAC=BDDC
Area=12×base×height
For triangle ABD, the base is BD and the height is the perpendicular dropped from A to line BD. For triangle ACD, the base is DC and the height is the same perpendicular from A.
- Area of triangle ABD:
AreaABD=12×BD×h
- Area of triangle ACD:
AreaACD=12×DC×h
Now we can find the ratio of the areas of triangles ABD and ACD:
AreaABDAreaACD=12×BD×h12×DC×h
Here, the 12 and h cancel out:
AreaABDAreaACD=BDDC
From the angle bisector theorem, we know that:
BDDC=ABAC
Therefore, we can conclude:
AreaABDAreaACD=ABAC
AreaABDAreaACD=ABAC
Topper's Solved these Questions
- TRIANGLES Book:MTG IIT JEE FOUNDATIONChapter:TRIANGLES Exercise: Exercise (Multiple Choice Questions) (LEVEL -2)
Explore 15 Videos
- TRIANGLES Book:MTG IIT JEE FOUNDATIONChapter:TRIANGLES Exercise: Exercise (Match the following )
Explore 3 Videos
- TRIANGLES Book:MTG IIT JEE FOUNDATIONChapter:TRIANGLES Exercise:NCERT Section Exercise 6 .6
Explore 12 Videos
- SURFACE AREAS AND VOLUMESBook:MTG IIT JEE FOUNDATIONChapter:SURFACE AREAS AND VOLUMESExercise:OLYMPIAD/HOTS CORNER
Explore 20 Videos
Similar Questions
Knowledge Check
In ΔABC,AB=5cm,AC=7cm. If AD is the angle bisector of ∠A Then BD:CD is :
A25:49B49:25C6:1D5:7ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then, ar(ΔBDE)=12ar(ΔABC).
ATrueBFalseCPartially trueDNone of these
In the ΔABC , MN||BC and AM : : MB = 13.
Then, ar(ΔAMN)ar(ΔABC)=?
View SolutionIn ΔABC, if AD is the bisector of ∠A, show that AB>BDandAC>DC.
View SolutionIn ΔABC,ADandBE are altitudes. Prove that ar(ΔDEC)ar(ΔABC)=DC2AC2.
View SolutionIn ΔABC,AD is the bisector of ∠A. Write AB, BD and DC in descending order of their length.

View SolutionIn an equilateral ΔABC,D is the midpoint of AB and E is the midpoint of AC. Then, ar(ΔABC):ar(ΔADE)=?

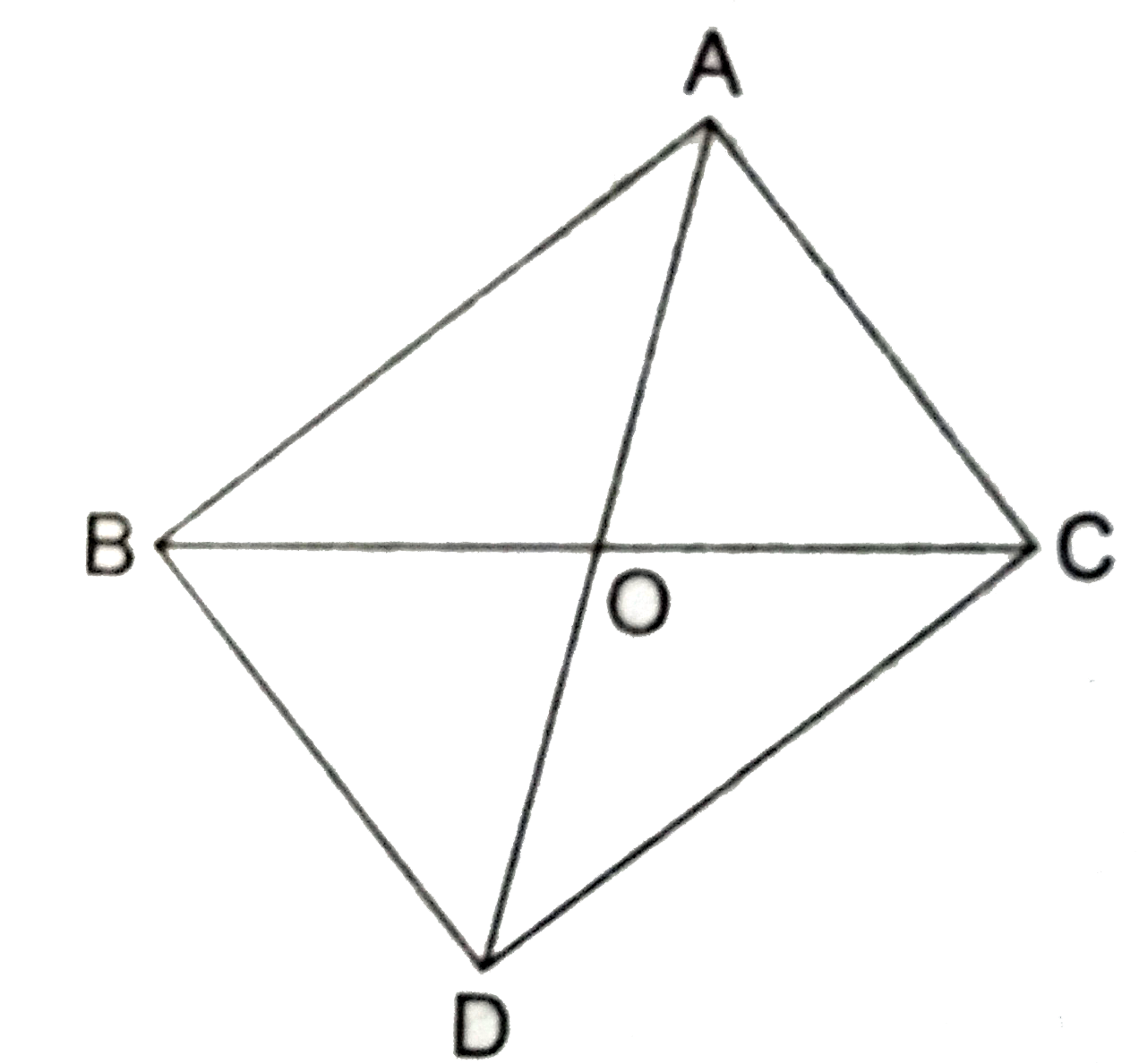
View SolutionIn the given figure, ΔABCandΔDBC have the same base BC. If AD and BC intersect at O, prove that ar(ΔABC)ar(ΔDBC)=AODO
View Solution