In Fig. 10.39, A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠BEC\ =\ 130o and ∠ECD\ =\ 20⊙ Find ∠BAC.
Step by step video & image solution for In Fig. 10.39, A, B, C and D are four points on a circle. AC and BD intersect at a point E such that /_B E C"\ "="\ "130o and /_E C D"\ "="\ "20odot Find /_B A Cdot by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
A, B, C, D are four points on a circle. AC and BD intersect at a point E such that ∠BEC=130∘and∠ECD=20∘.∠BAC is
A(A) 120B(B)90∘C(C)100∘D(D)110∘
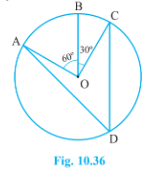
In Fig. 10.36, A,B and C are three points on a circle with centre O such that ∠BOC= 30o and ∠AOB= 60o. If D is a point on the circle other than the arc ABC, find ∠ADC.
 View Solution
View SolutionA, B, C, D are four consecutive points on a circle such that AB=CD. Prove that AC=BD
View SolutionD and E are points on sides AB and AC respectively of ΔABCsuch thatar (DBC) = ar (EBC). Prove that DE ∣∣ BC.
View SolutionIn Fig. 71, if ABCD and CDEF, find ∠ACE
View SolutionIn fig. 10, A,B,C and D are four points, and no three points are collinear. AC and BD intersect at O. there are eight triangle that you can observe. Name all the triangles.
View SolutionIn a ABC,D and E are points on sides ABandAC respectively such that BD=CE. If ∠B=∠C, show that DEBC.
View SolutionABC is a triangle. D is a point on AB such that D=14AB and E is a point on AC such that AE=14AC. Prove that DE=14BC
View Solution

