In Fig. 12.33, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
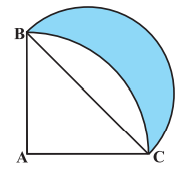
To find the area of semi-circle, we need to find the radius or diameter (BC) of the semicircle.
△ABC is a right-angled triangle, right-angled at A (ABC being a quadrant).
AB=AC=14cm [Radius of the circle]
Using Pythagoras theorem, we can find the hypotenuse (BC) of △ABC.
BC2=AB2+AC2
= (14cm)2+(14cm)2
BC = (√2)×(14cm)2
= 14√2cm
Radius of semicircle BDC, r=BC2=14√22cm=7√2cm
Area of the shaded region = Area of semicircle - (Area of quadrant ABC - Area △ABC)
= πr22−[90∘360∘×π(14)2−12×AC×AB]
= (π(7√2))22−[(π(14))24−12×14×14]
= [22×7×7×27×2]−[22×14×147×4−7×14]
= 154−(154−98)
= 98cm2
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - EXERCISE 12.15videos
AREAS RELATED TO CIRCLES
- BOOK - NCERTCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - SOLVED EXAMPLES6videos
AREAS RELATED TO CIRCLES
- BOOK - NCERTCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - SOLVED EXAMPLES6videos
AREAS RELATED TO CIRCLES
- BOOK - NCERTCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - Exercise 5.320videos
ARITHMETIC PROGRESSIONS
Similar Questions
In Fig. 12.33, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
 View Solution
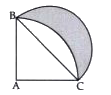
View SolutionIn the given figure, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
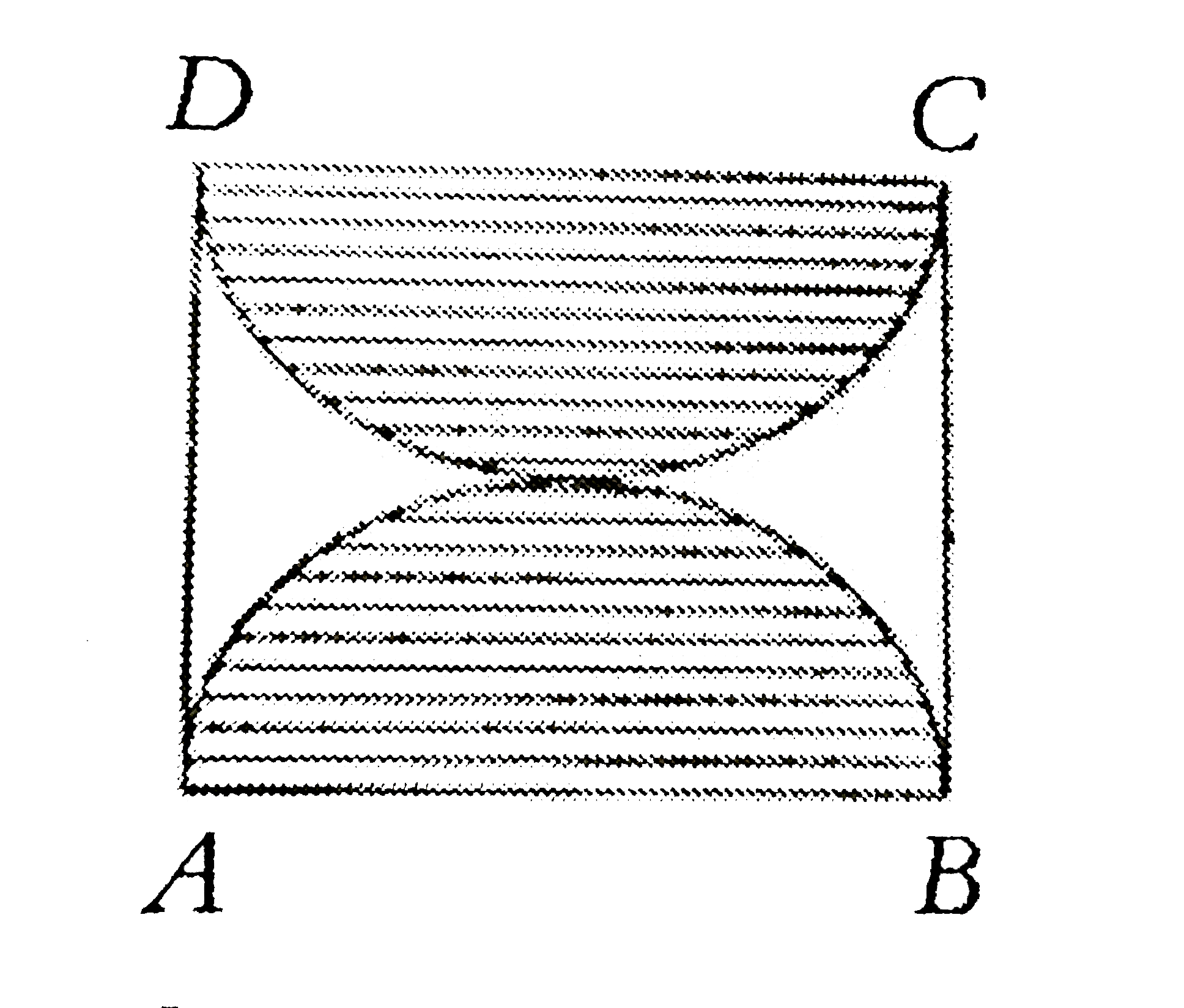
In the adjoining figure, ABCD is a square of side 7 cm and two semicircles are drawn inside of it with AB and CD as diameters. Find the area of the shaded region (in cm2).
 A144 m2B164 m2C184 m2D154 m2
A144 m2B164 m2C184 m2D154 m2
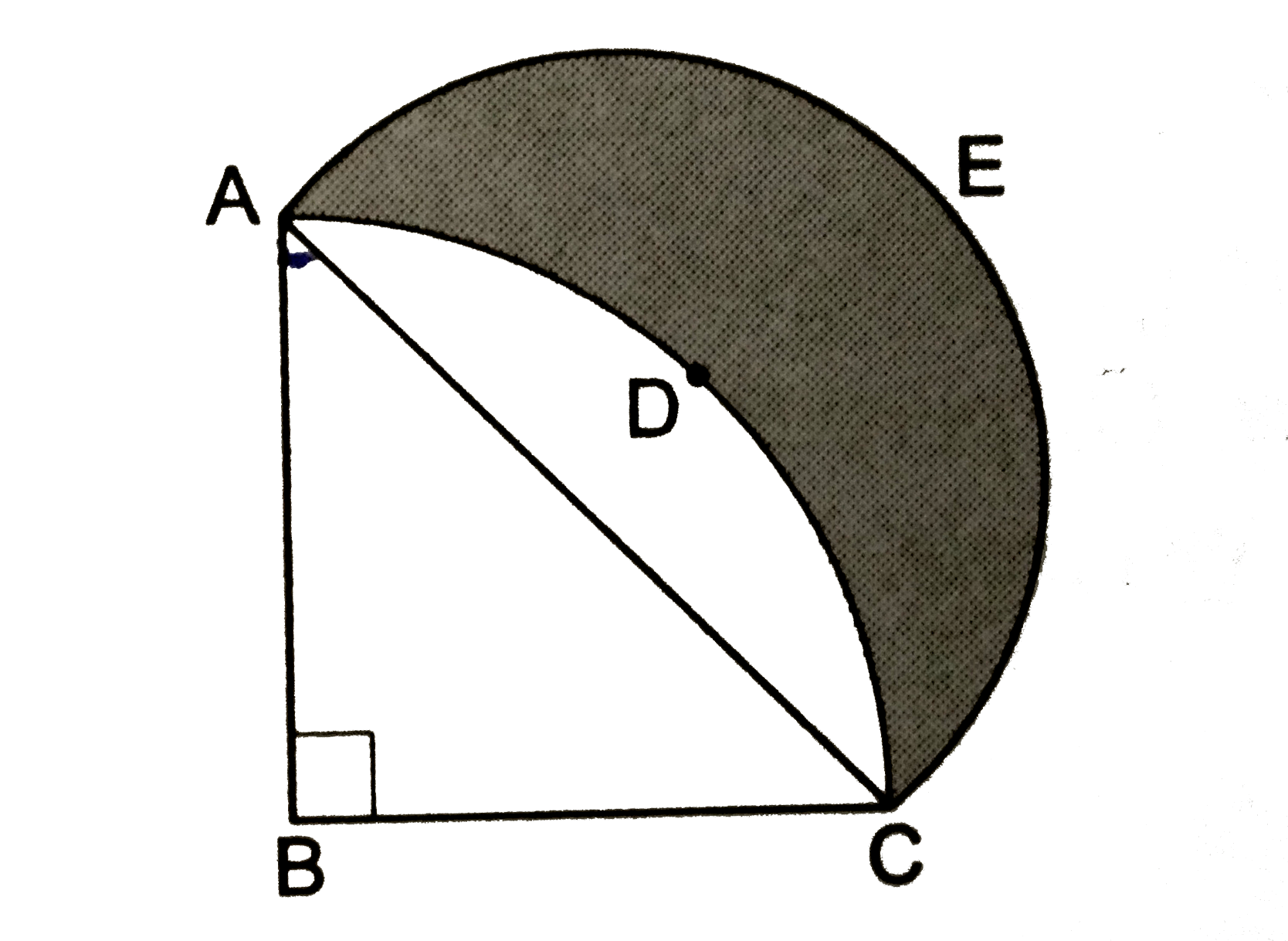
In the given figue, ABCD is a quadrant of a circle of radius 28 cm and a semicircle ABECA is drawn with AC as diameter. Find the area of the shaded region.
 View Solution
View SolutionIn figure ABDC is a quadrant of a circle of a radius 28 cm and a semi circles BEC is drawn with BC as diameter find the area of shaded region:
View SolutionABCP is a quadrant of a circle of radius 14 cm. with AC as diameter, a semicircle is drawn. Find the area of the shaded portion
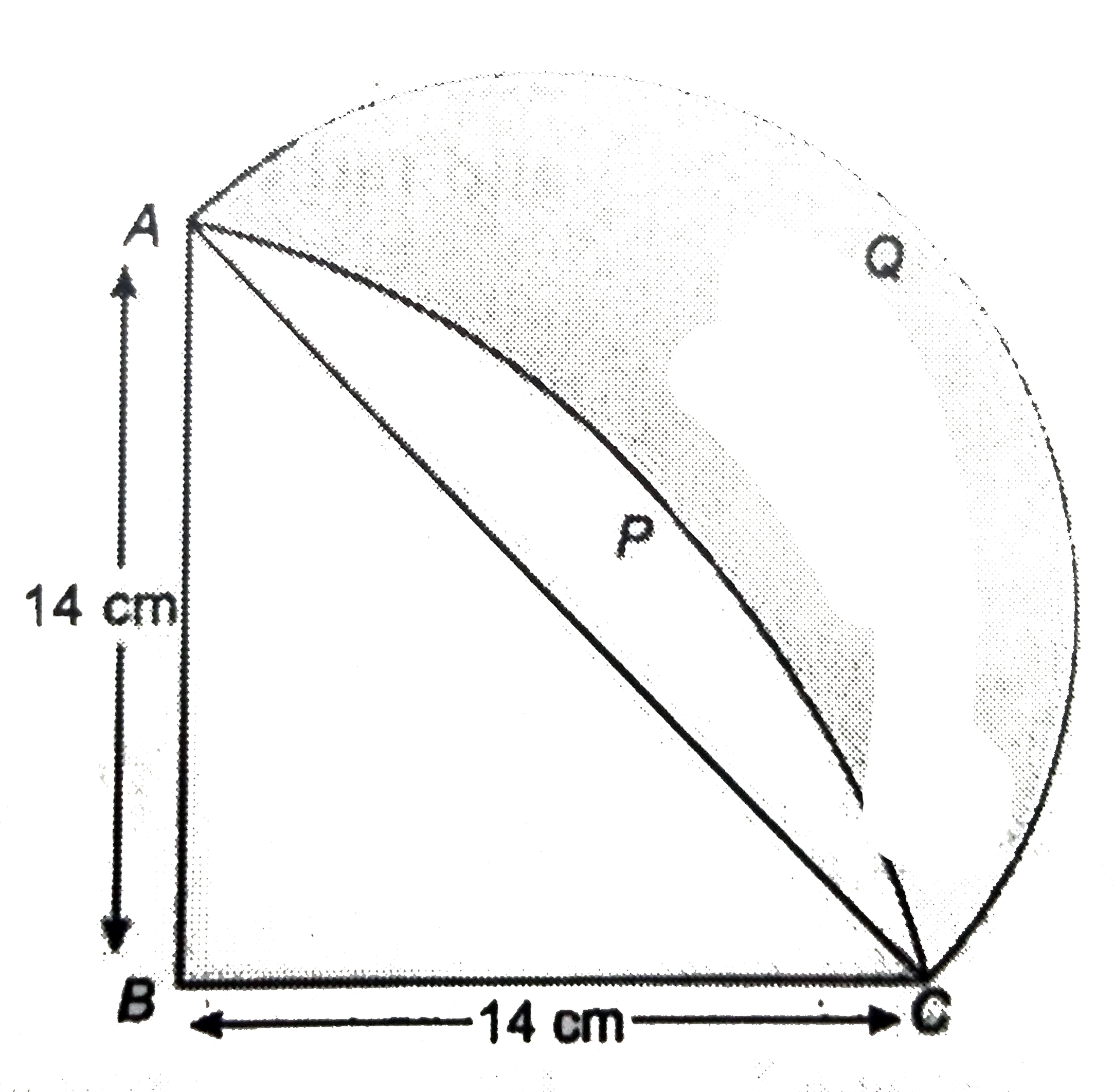 View Solution
View SolutionBCP is a quadrant of a circle of radius 14cm. With AC as diameter, a semi-circle is drawn. Find the area of the shaded portion.
View SolutionABCP is a quadrant of a circle of radius 14 cm. With AC as diameter, a semi-circle is drawn. Find the area of the shaded portion.
View SolutionIn Fig. 12.64, ABCP is a quadrant of a circle of radius 20 cm. With AC as diameter, a semi-cirde is drawn. Find the area of the shaded portion.
 View Solution
View SolutionIn the given figure, ABCD is a square of side 10 cm and semicircles are drawn with each side of the square as diameter. Find the area of the shaded region.
[ Use π=3.14]
 View Solution
View Solution

