In Fig. 4.170, is a trapezium in which and . Determine the ratio of the areas of and . (FIGURE)
In .
( vertically opposite angles)
(alternate angles as AB||DC)
(AA corollary)
( ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding sides)
( AB= 2CD, given)

Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Problems From NCERT/ Exemplar
14 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Exercise 6a
23 Videos
- STATISTICS BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
5 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHANCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
In Figure, ABCD is a trapezium in which AB∣∣CD . Prove that: ar(AOD)=ar(BOC).

View SolutionD, E, F are the mid-points of the sides BC, CA and AB respectively of a ABC . Determine the ratio of the areas of DEF and ABC .
View SolutionIn Figure, ABCD is a trapezium in which ABCD and AD=BC. show that : ∠A=∠B (ii) ∠C=∠D ABC≅BAD diagonal AC=diagonalBD
View SolutionIn Figure, ABCD is a trapezium in which AB=7cm, AD=BC=5cm, DC=x cm, and distance between AB and DC is 4cm . Find the value of x and area of trapezium ABCD
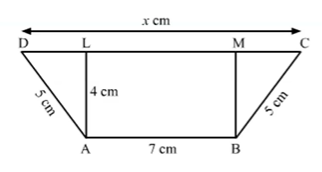
View SolutionIn Fig. 15.63, ABCD is a trapezium with ABDC and ∠BCD=60o . If BFEC is a sector of a circle with centre C and AB=BC=7 cm and DE=4 cm , then find the area of the shaded region (Use π=227 and √3=1.732) .
View SolutionABCD is a trapezium in which ABDC. If ar(ABD)=24 cm2and AB=8 cm, then height of ABC is 3 cm (b) 4 cm (c) 6 cm (d) 8 cm
View SolutionIn Figure, ABCD is a trapezium in which AB∣∣DC, DC is produced to E such that CE=AB, prove that ar(ABD)=ar (BCE). Construction: Draw DM on BA produced and BN⊥DC

View SolutionIn Fig. 4.179, ABC and DBC are on the same base BC . If AD and BC intersect at O , prove that Area (ABC)Area (DBC)=AODO (FIGURE)
View SolutionABCD is a trapezium with AB∣∣DC . A line parallel to AC intersects AB at X and BC at Y. Prove that ar(ADX)=ar(ACY).
View SolutionIn figure, ABC is a triangle in which ∠ABC=90∘and AD⊥BC. Prove that AC2=AB2+BC2−2BC.BD.

View Solution
