In Fig. 63, line l ∣∣ m and a transversal n cuts them at P and Q respectively. If ∠1=750, find all other angles.
To solve the problem, we will use the properties of angles formed by parallel lines and a transversal. Let's denote the angles as follows based on the figure:
- Angle 1 = ∠1
- Angle 2 = ∠2
- Angle 3 = ∠3
- Angle 4 = ∠4
- Angle 5 = ∠5
- Angle 6 = ∠6
- Angle 7 = ∠7
- Angle 8 = ∠8
Given that ∠1 = 75°, we will find the measures of all other angles step by step.
Step 1: Find Angle 2
Since ∠1 and ∠2 are a linear pair (they are on the same line), we can use the fact that the sum of angles on a straight line is 180°.
Angle 2=180°−Angle 1=180°−75°=105°
Step 2: Find Angle 4
Angle 2 and Angle 4 are vertically opposite angles. Therefore, they are equal.
Angle 4=Angle 2=105°
Step 3: Find Angle 3
Angle 1 and Angle 3 are also vertically opposite angles. Therefore, they are equal.
Angle 3=Angle 1=75°
Step 4: Find Angle 5
Angle 1 and Angle 5 are corresponding angles (since l || m and n is the transversal). Therefore, they are equal.
Angle 5=Angle 1=75°
Step 5: Find Angle 6
Angle 2 and Angle 6 are also corresponding angles. Therefore, they are equal.
Angle 6=Angle 2=105°
Step 6: Find Angle 7
Angle 5 and Angle 7 are vertically opposite angles. Therefore, they are equal.
Angle 7=Angle 5=75°
Step 7: Find Angle 8
Angle 6 and Angle 8 are vertically opposite angles. Therefore, they are equal.
Angle 8=Angle 6=105°
Summary of Angles
- ∠1 = 75°
- ∠2 = 105°
- ∠3 = 75°
- ∠4 = 105°
- ∠5 = 75°
- ∠6 = 105°
- ∠7 = 75°
- ∠8 = 105°
- Angle 2 = ∠2
- Angle 3 = ∠3
- Angle 4 = ∠4
- Angle 5 = ∠5
- Angle 6 = ∠6
- Angle 7 = ∠7
- Angle 8 = ∠8
Since ∠1 and ∠2 are a linear pair (they are on the same line), we can use the fact that the sum of angles on a straight line is 180°.
Angle 2 and Angle 4 are vertically opposite angles. Therefore, they are equal.
Angle 1 and Angle 3 are also vertically opposite angles. Therefore, they are equal.
Angle 1 and Angle 5 are corresponding angles (since l || m and n is the transversal). Therefore, they are equal.
Angle 2 and Angle 6 are also corresponding angles. Therefore, they are equal.
Angle 5 and Angle 7 are vertically opposite angles. Therefore, they are equal.
Angle 6 and Angle 8 are vertically opposite angles. Therefore, they are equal.
- ∠1 = 75°
- ∠2 = 105°
- ∠3 = 75°
- ∠4 = 105°
- ∠5 = 75°
- ∠6 = 105°
- ∠7 = 75°
- ∠8 = 105°
Topper's Solved these Questions
Similar Questions
In Fig. 64, AB∣∣CD and a transversal PQ cuts them at L and M respectively. If ∠QMD=1000, find all other angles.
View SolutionIn Fig.59, AB and CD are parallel lines intersected by a transversal PQ at L and M respectively, If ∠CMQ=600 find all other angles in the figure.
View SolutionIn Fig.22, it being that ∠1=650, find all other angles.
View SolutionIn Fig. 5.55, l ||m and a line t intersects these lines at P and Q, respectively. Find the sum 2a + b.
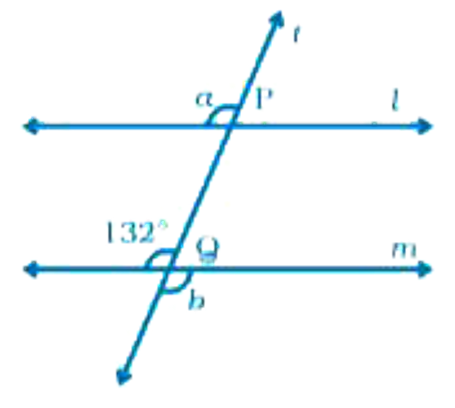 View Solution
View SolutionA line l is parallel to line m and a transversal p interesects them at X, Y respectively. Bisectors of interior angles at X and Y interesct at P and Q. Is PXQY a rectangle? Given reason.
View SolutionIn Fig. 60, AB and CD are parallel lines intersected by a transversal PQ at L and M respectively. If ∠LMD=350 find ∠PLA.
View SolutionIn Fig. 62, line l∣∣m and n is a transversal. If ∠1=400, find all the angles and check that all corresponding angles and alternate angles are equal.
View SolutionIn the given figure, p ll q and t is the transversal. If ∠1=110∘, find the other angles.
View SolutionIn Fig.99, ABCD and EF is a transversal intersecting AB and CD at P and Q respectively. The measure of ∠DPQ is (a) (b)(c)(d)(e)100(f)0(g)(h)(i) (j) (b) (k)(l)(m)(n)80(o)0(p)(q)(r) (s) (c) (d)(e)(f)(g)110(h)0(i)(j)(k) (l) (d) (m)(n)(o)(p)70(q)0(r)(s)(t) (u)
View SolutionIn Fig. l, m and n are parallel lines intersected by transversal p at X, Y and Z respectively. Find ∠1, ∠2 and ∠3
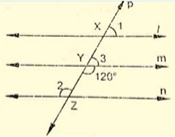 View Solution
View Solution

