In Fig. 6.38, the sides AB and AC of ABC are produced to points E and D respectively. If bisectors BO and CO of CBE and BCD respectively meet at point O, then prove that ∠BOC=90∘−12∠BAC..
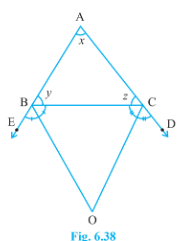
∠CBE=180−∠ABC
∠CBO=12∠CBE (BO is the bisector of ∠CBE)
∠CBO=12(180−∠ABC)
12x180=90
∠CBO=90−12∠ABC .............(1)
12x∠ABC=12∠ABC
∠BCD=180−∠ACD
∠BCO=12∠BCD ( CO is the bisector Is ∠BCD)
∠BCO=12(180−∠ACD)
∠BCO=90−12∠ACD ............(2)
∠BOC=180−(∠CBO+∠BCO)
∠BOC=180−(90−12∠ABC+90−12∠ACD)
∠BOC=180−180+12∠ABC+12∠ACD
∠BOC=12(∠ABC+∠ACD)
∠BOC=12(180−∠BAC)(180−∠BAC=∠ABC+∠ACD)
∠BOC=90−12∠BAC
Topper's Solved these Questions
Similar Questions
In Fig. 6.38, the sides AB and AC of ABC are produced to points E and D respectively. If bisectors BO and CO of CBE and BCD respectively meet at point O, then prove that ∠BOC=90∘−12∠BAC..

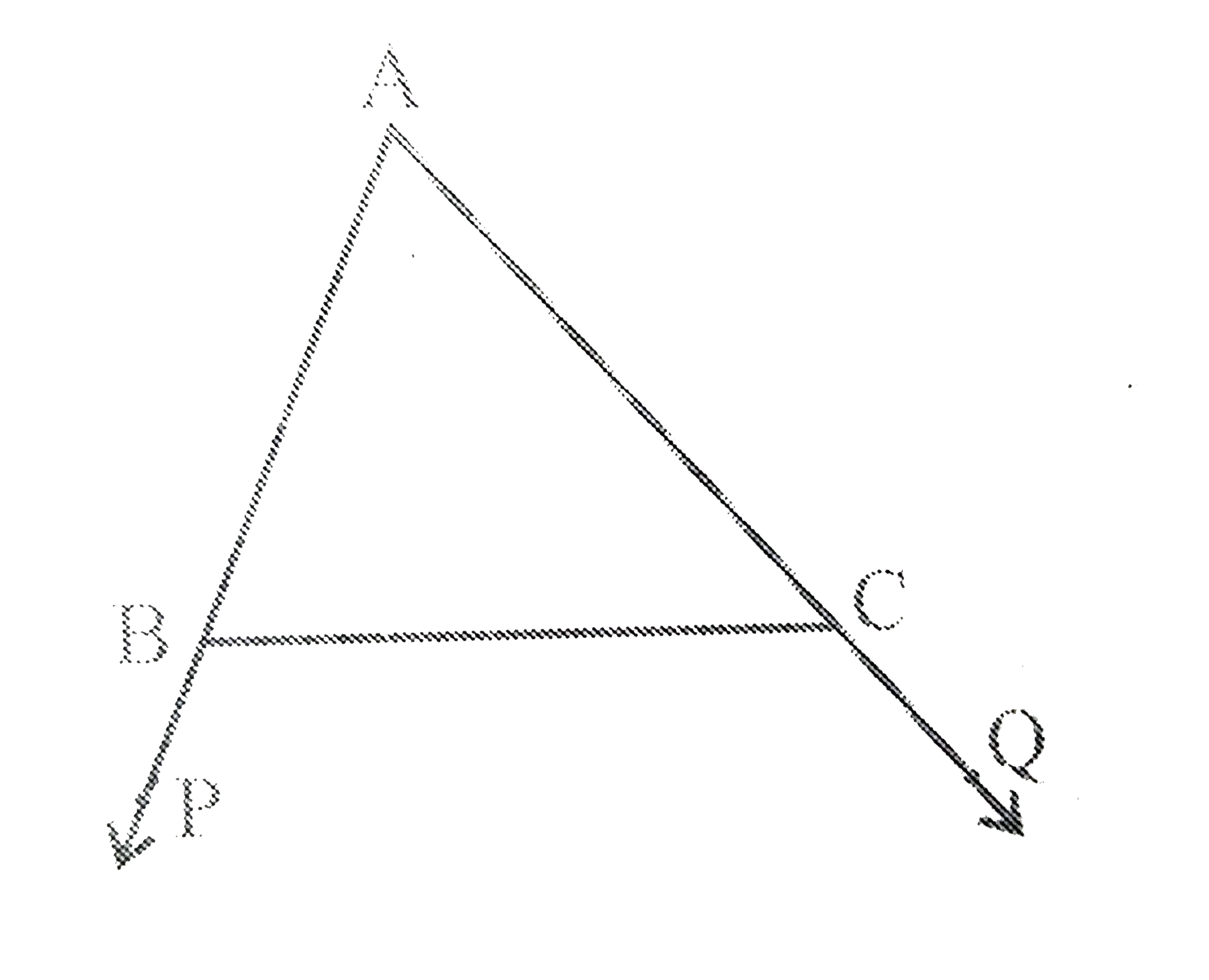
View SolutionIn Fig. 7.48, sides ABandAC of ΔABC are extended to points PandQ respectively. Also, ∠PBC <∠QCB. Show that AC > AB.
View Solution
Knowledge Check
If ΔABC,∠A=52∘, Its sides AB and AC are produced to the points D and E respectively. If the bisectors of the ∠CBDand∠BCE meet at point O, then ∠BOC is equal to:
A106∘B64∘C16∘D32∘In figure, sides AB and AC of a ΔABC are produced to P and Q, respectively. The bisectors of <PBC and <QCB intersect at O. Tnen. <BOC is equal to
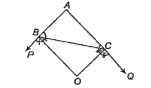 A90∘−12<BACB12(<PBC+<QCB)C90∘+12<BACDNone of the above
A90∘−12<BACB12(<PBC+<QCB)C90∘+12<BACDNone of the aboveIn figure, sides AB and AC of a ΔABC are produced to P and Q, respectively. The bisectors of ∠PBCand∠QCB intersect at O. Then, ∠BOC is equal to
 A90∘−12∠BACB12(∠PBC+∠QCB)C90∘+12∠BACDNone of the above
A90∘−12∠BACB12(∠PBC+∠QCB)C90∘+12∠BACDNone of the above
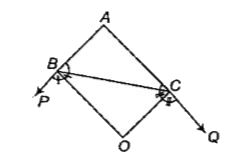
The sides AB and AC of ABC are product to P and Q respectively. the bisectors of exterior angles at B and C of ABC meet at O (fig.19) prove that ∠BOC=900−12∠A
View SolutionIn △ABC ,∠A=72∘. Its sides AB and AC are produced to the point D and E. If the bisectors of the ∠CBD and ∠BCE meet at the point O, then ∠BOC will be equal to:
त्रिभुज ABC में, ∠A=72∘ है | इसकी भुजाओं AB और AC को बिंदु D तथा E तक बढ़ाया जाता है | यदि कोण CBD और कोण BCE के समद्विभाजक बिंदु O पर मिलते हैं, तो ∠BOC का मान ज्ञात करें |
View SolutionThe sides AB and AC of △ABC are produced to points D and E, respectively. The bisectors of ∠CBDand∠BCE meet at P. If ∠A=72∘, then the measure of ∠P is:
View SolutionThe sides AB and AC of a ΔABC are produced to P and Q respectively. If the bisectors of ∠PBC and ∠QCB meet at O ; Then ∠BOC=90∘−12∠A
View SolutionIn a △ABC, ∠A=52∘. Its sides AB and AC are produced to the points D and E respectively. If the bisectors of the ∠CBD and ∠BCE meet at point O, then ∠BOC is equal to:
△ABC में ∠A=52∘ है। इनकी भुजाएं AB और AC क्रमशः D और E तक बढाई जाती है। अगर ∠CBD और ∠BCE समदूविभाजक बिंदु O पर मिलते हैं, तो ∠BOC बराबर हैः
View Solution
