Question

In Fig. 6.40, $\angle X={62}^{\circ },$$\angle XYZ={54}^{\circ }$. If YO and ZO are the bisectors of $\angle XYZ$ and $\angle XZY$ respectively of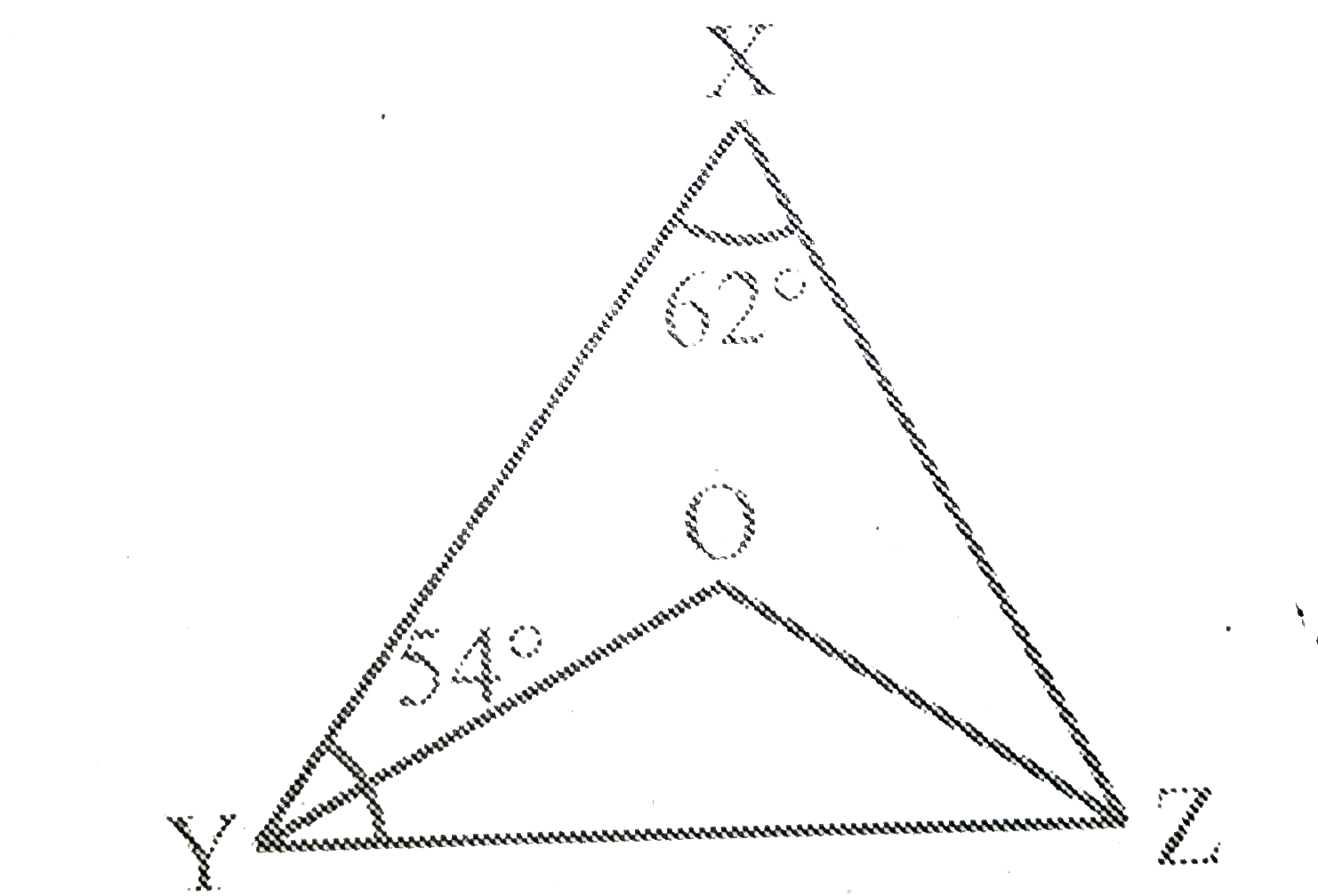 $\Delta XYZ,$ find $\angle OZY$ and $\angle YOZ$.

Explanation

As the sum of all interior angles of a triangle is 180º, therefore, for ΔXYZ,


∠X + ∠XYZ + ∠XZY = 180º


62º + 54º + ∠XZY = 180º


∠XZY = 180º − 116º


∠XZY = 64º


∠OZY = 32º (OZ is the angle bisector of ∠XZY)


Similarly, ∠OYZ == 27º


Using angle sum property for ΔOYZ, we obtain


∠OYZ + ∠YOZ + ∠OZY = 180º


27º + ∠YOZ + 32º = 180º


∠YOZ = 180º − 59º


∠YOZ = 121º