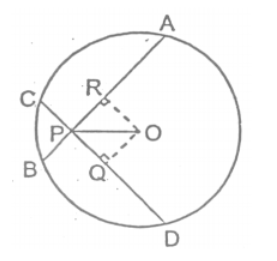
In Figure, is the centre of the circle. Prove that bisects
Join
(Radii of the same circle)
(Given)
(Common)
(BY SSS
(C.P.CT.)
.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure (not to scale ) , O is the centre of the circle . A ,B,C and D are conyclic and AB =CD . If ∠MON=120∘ , then find ∠OPN .
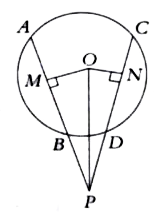 A20∘B30∘C40∘D60∘
A20∘B30∘C40∘D60∘
In Figure, AB is a diameter of the circle such that ∠A=350and ∠Q=250, find ∠PBR
View SolutionIn Figure, O is the centre of the circle such that ∠AOC =1300, then ∠ABC= 1300 (b) 1150 (c) 650 (d) 1650
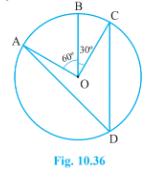
View SolutionIn Fig. 10.36, A,B and C are three points on a circle with centre O such that ∠BOC= 30o and ∠AOB= 60o. If D is a point on the circle other than the arc ABC, find ∠ADC.
 View Solution
View SolutionA quadrilateral ABCD is such that diagonal BD divides its area in two equal parts. Prove that BD bisects AC. GIVEN : A quadrilateral ABCD in which diagonal BD bisects it. i.e. ar(ABD)=ar(BDC) CONSTRUCTION : Join AC Suppose AC and BD intersect at O . Draw AL⊥BD and CMBD. TO PROVE : AO=OC.
View SolutionIn Figure, O and O' are centres of two circles intersecting at B and C.ACD is a straight line, find x
View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
 View Solution
View SolutionIn Figure, O is the centre of the circle and ∠BDC=420. The measure of ∠ACB is 420 (b) 480 (c) 580 (d) 520
View Solution