In figure, AD is a median of a triangle ABC and AM⊥BC. Prove that:
(i) AC2=AD2+BC.DM+(BC2)2
(ii) AB2=AD2−BC.DM+(BC2)2
(iii) AC2+AB2=2AD2+12BC2
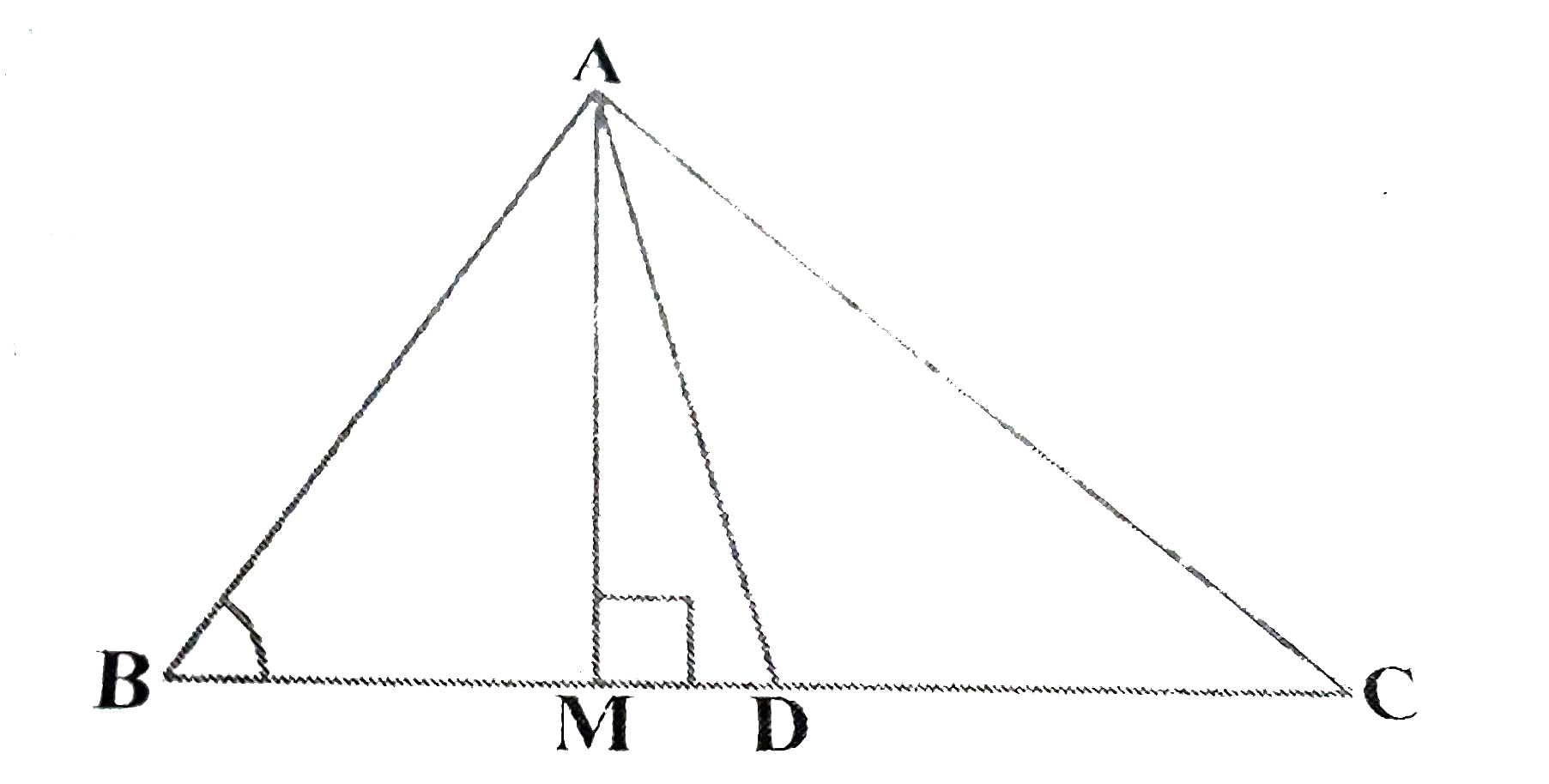
Given:
In ΔABC,ADis a median, AM⊥BC.
To Prove
(i) (AC)2=(AD)2+BC.DM+(BC2)2
(ii) (AB)2=(AD)2–BC.DM+(BC2)2
(iii) (AC)2+(AB)2=2(AD)2+12(BC)2
Proof:
i) In obtuse ΔADC,∠D>90∘
(AC)2=(AD)2+(DC)2+2DC.DM
(AC)2=(AD)2+(BC2)2+2(BC2).DM
(AC)2=(AD)2+(BC2)2+BC.DM
Or (AC)2=(AD)2+BC.DM+(BC2)2
II)In acute triangle ABD,
∠D>90∘
(AB)2=(AD)2+(BD)2+2BD.DM
(AB)2=(AD)2+(BC2)2−2(BC2).DM
(AB)2=(AD)2+(BC2)2−BC.DM
Or
(AB)2=(AD)2−BC.DM+(BC2)2
iii) Adding i and ii
(AC)2+(AB)2=(AD)2+BC.DM+(BC2)2+(AD)2−BC.DM+(BC2)2
=2(AD)2+BC42+BC42
=2(AD)2+12.BC42
=2(AD)2+(BC)2
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - TRIANGLESEXERCISE - EXERCISE 6.316videos
TRIANGLES
- BOOK - NCERTCHAPTER - TRIANGLESEXERCISE - SOLVED EXAMPLES14videos
TRIANGLES
- BOOK - NCERTCHAPTER - TRIANGLESEXERCISE - Exercise 6.210videos
TRIANGLES
- BOOK - NCERTCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - EXERCISE 13.28videos
SURFACE AREAS AND VOLUMES
Similar Questions
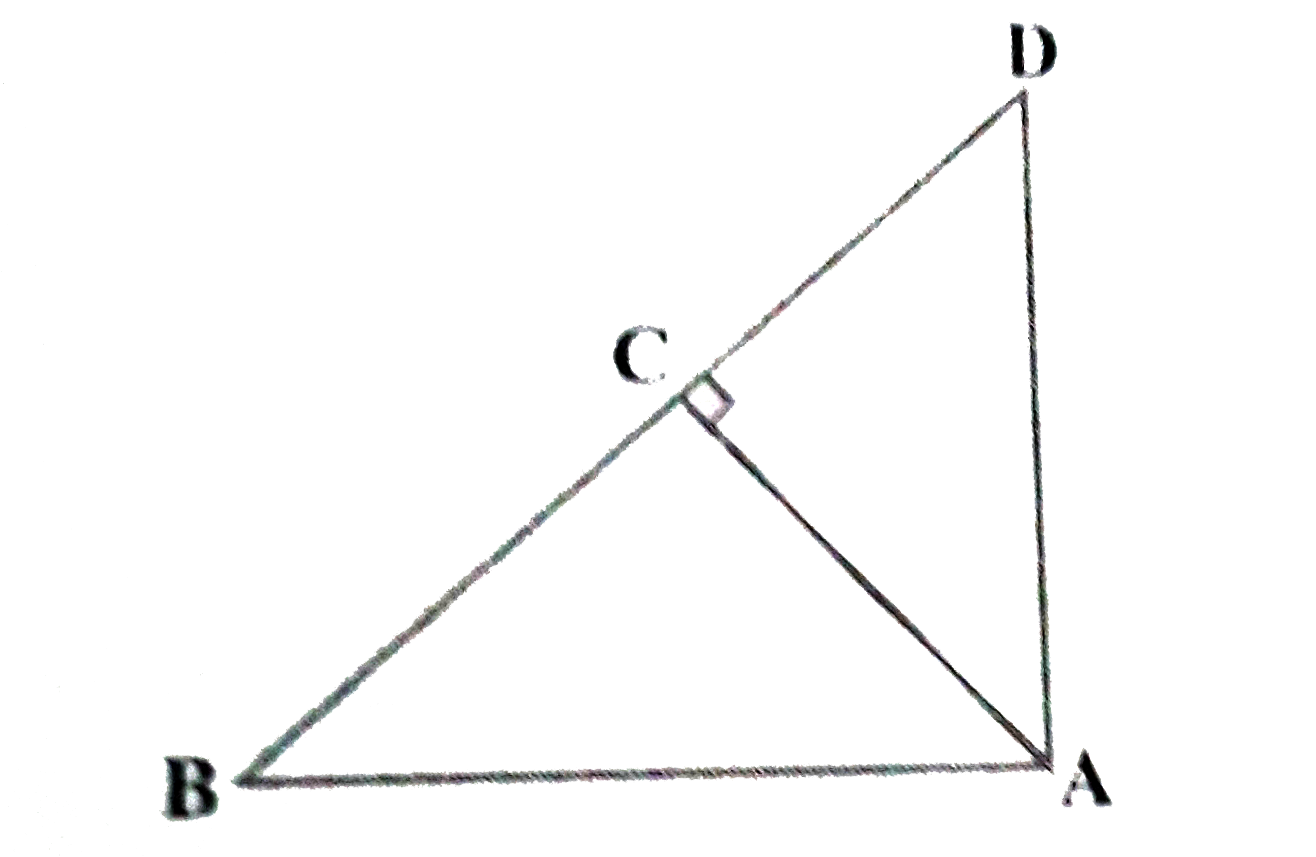
In figure, ABC is a triangle in which ∠ABC=90∘and AD⊥BC. Prove that AC2=AB2+BC2−2BC.BD.
 View Solution
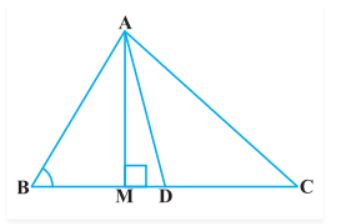
View SolutionIn Figure, ABD is a triangle right-angled at A and AC⊥BD. Show that
(i)AB2=BC.BD
(ii) AC2=BC.DC
(iii) AD2=BD.CD
 View Solution
View SolutionIn figure, ABC is triangle in which ∠ABC=90∘and AD⊥CBproduced. Prove that AC2=AB2+BC2−2BC.BD.
 View Solution
View SolutionIn ABC , AD is a median. Prove that AB2+AC2=2 AD2+2 DC2 .
View SolutionIn figure, O is a point in the interior of a triangle ABC, OD⊥BC,OE⊥ACand OF⊥AB. Show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AW2+CD2+BF2
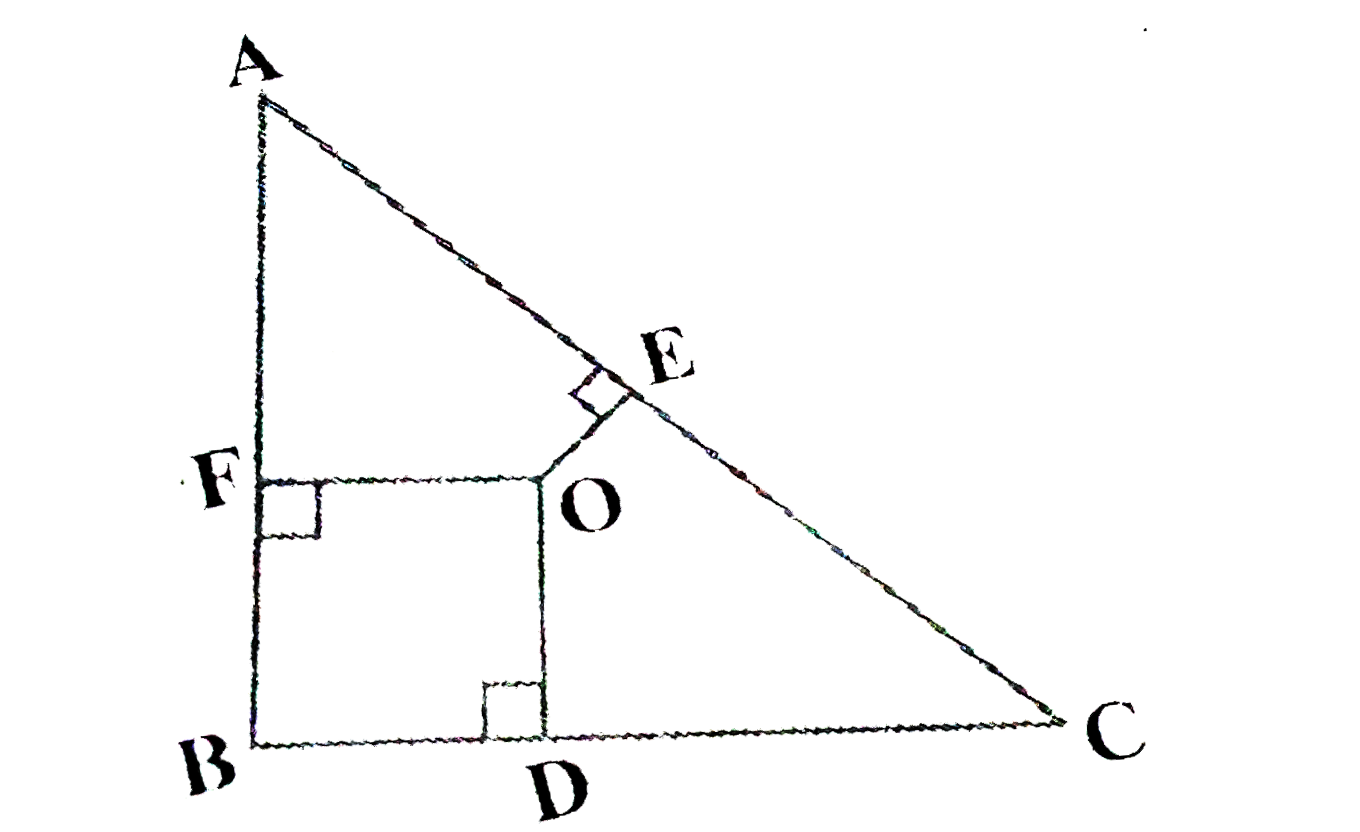 View Solution
View SolutionIn a quadrilateral ABCD , given that ∠A+∠D=90o . Prove that AC2+BD2=AD2+BC2 .
View SolutionABD is a right triangle right-angled at A and AC⊥BD . Show that AB2=BC.BD (ii) AC2=BC.DC (iii) AD2=BD.CD (iv) AB2AC2=BDDC
View SolutionIn an equilateral triangle ABC if AD⊥BC, then AD2 = (a)CD2 (b) 2CD2 (c) 3CD2 (d) 4CD2
View SolutionIn a triangle ABC , right angled at B, the inradius is AB+BC−AC2 (b) AB+AC−BC2 AB+BC+AC2 (d) none
View SolutionIn Fig. 4.220, D is the mid-point of side BC and AE⊥BC . If BC=a, AC=b, AB=c, ED=x, AD=p and AE=p and AE=h , prove that: (FIGURE) b2=p2+ax+a24 (ii) c2=p2−ax+a24 (iii) b2+c2=2 p2+a22
View Solution

