In Figure, determine ∠P+∠Q+∠R+∠S+∠T.
To determine the sum of angles ∠P+∠Q+∠R+∠S+∠T in the given pentagon ABCDE, we can follow these steps:
1. Identify the Pentagon: Recognize that ABCDE is a pentagon. The sum of the interior angles of a pentagon can be calculated using the formula:
Sum of interior angles=(n−2)×180∘
where n is the number of sides. For a pentagon, n=5.
2. Calculate the Sum of Interior Angles:
Sum of interior angles=(5−2)×180∘=3×180∘=540∘
3. Understanding the Angles: The angles ∠P,∠Q,∠R,∠S, and ∠T are the interior angles of the pentagon ABCDE.
4. Using the Properties of Angles: Since the sum of the interior angles of the pentagon is 540∘, we can express this as:
∠P+∠Q+∠R+∠S+∠T=540∘
5. Conclusion: Therefore, the sum of the angles ∠P+∠Q+∠R+∠S+∠T is:
540∘
Sum of interior angles=(n−2)×180∘
where n is the number of sides. For a pentagon, n=5.
Sum of interior angles=(5−2)×180∘=3×180∘=540∘
∠P+∠Q+∠R+∠S+∠T=540∘
540∘
Topper's Solved these Questions
Similar Questions
In Figure, OP∣∣RS. Determine ∠PQR
View SolutionIn Figure, PS=QR and ∠SPQ=∠RQP. Prove that PQS ≅ QPR, PR=QS and ∠QPR= ∠PQS
View SolutionIn Figure, PS=PR, ∠TPS= ∠QPR. Prove that PT=PQ
View SolutionIn Figure, ∠PQR= ∠PRQ, then prove that ∠PQS= ∠PRT.
View SolutionIf Figure, if QT⊥PR,∠TQR=400 AND ∠SPR=300, find x and y. Figure
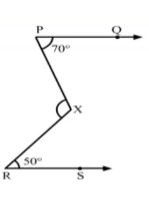
View SolutionIn Figure , find out ∠PXR, if PQ ∣∣ RS.
View SolutionIn Figure, if PQ⊥PS, PQSR, ∠SQR=280and ∠QRT=650, then find the values of x and y
View SolutionIn Figure, if quadrilateral PQRS circumscribes a circle, then PD+QB= (a)PQ (b) QR (c) PR (d) PS
View SolutionIn Figure, TQ and TR are the bisectors of ∠Q and ∠R respectively. If ∠QPR=800and ∠PRT=300, determine ∠TQR and ∠QTR
View SolutionIn Figure, if lines PQ and RS intersect at a point T such that ∠PRT=40∘, ∠RPT=95∘and ∠TSQ=75∘, find ∠SQT.
View Solution
