In Figure, O is the centre of the circle. Find ∠CBD
To find the angle ∠CBD in the given circle with center O, we can follow these steps:
1. Identify the Given Information:
- O is the center of the circle.
- The angle at the center ∠AOB (where A and B are points on the circumference) is given as 100 degrees.
2. Use the Angle at the Center Theorem:
- According to the theorem, the angle subtended at the center of the circle is twice the angle subtended at any point on the circumference.
- Therefore, if ∠AOB = 100 degrees, then the angle ∠ACB (where C is a point on the circumference) will be half of that.
∠ACB=12×∠AOB=12×100∘=50∘
3. Identify the Cyclic Quadrilateral:
- The points A, B, C, and P form a cyclic quadrilateral. In a cyclic quadrilateral, the opposite angles sum up to 180 degrees.
- Thus, we can write the equation:
∠ABC+∠P=180∘
4. Substitute the Known Angle:
- We know that ∠ACB = 50 degrees (from step 2). Therefore, we can substitute this value into the equation:
∠ABC+∠P=180∘
Rearranging gives:
∠ABC=180∘−∠P
5. Conclusion:
- Since ∠ABC is equivalent to ∠CBD, we can conclude that:
∠CBD=50∘
Final Answer:
∠CBD=50∘
- O is the center of the circle.
- The angle at the center ∠AOB (where A and B are points on the circumference) is given as 100 degrees.
- According to the theorem, the angle subtended at the center of the circle is twice the angle subtended at any point on the circumference.
- Therefore, if ∠AOB = 100 degrees, then the angle ∠ACB (where C is a point on the circumference) will be half of that.
- The points A, B, C, and P form a cyclic quadrilateral. In a cyclic quadrilateral, the opposite angles sum up to 180 degrees.
- Thus, we can write the equation:
- We know that ∠ACB = 50 degrees (from step 2). Therefore, we can substitute this value into the equation:
- Since ∠ABC is equivalent to ∠CBD, we can conclude that:
∠CBD=50∘
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In the figure , O is the centre of the circle and BCD is tangent to it at C . Find the value of ∠BAC+∠ACD
 A90∘B80∘C45∘D60∘
A90∘B80∘C45∘D60∘ - Question 2 - Select One
In the adjoining figure, O is the centre of the circle and D ∠OBD=50∘. Find the ∠BAD :
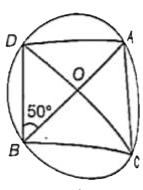 A60∘B40∘C80∘D45∘
A60∘B40∘C80∘D45∘ - Question 3 - Select One
In the given figure, O is the centre of the circle and ∠ACB=25∘ Find ∠AOB
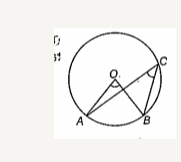 A25∘B50∘C75∘D60∘
A25∘B50∘C75∘D60∘
In Figure, O is the centre of the circle and ∠BDC=420. The measure of ∠ACB is 420 (b) 480 (c) 580 (d) 520
View SolutionIn the adjoining figure, O is the centre of the circle. Find the value of ∠BEC.
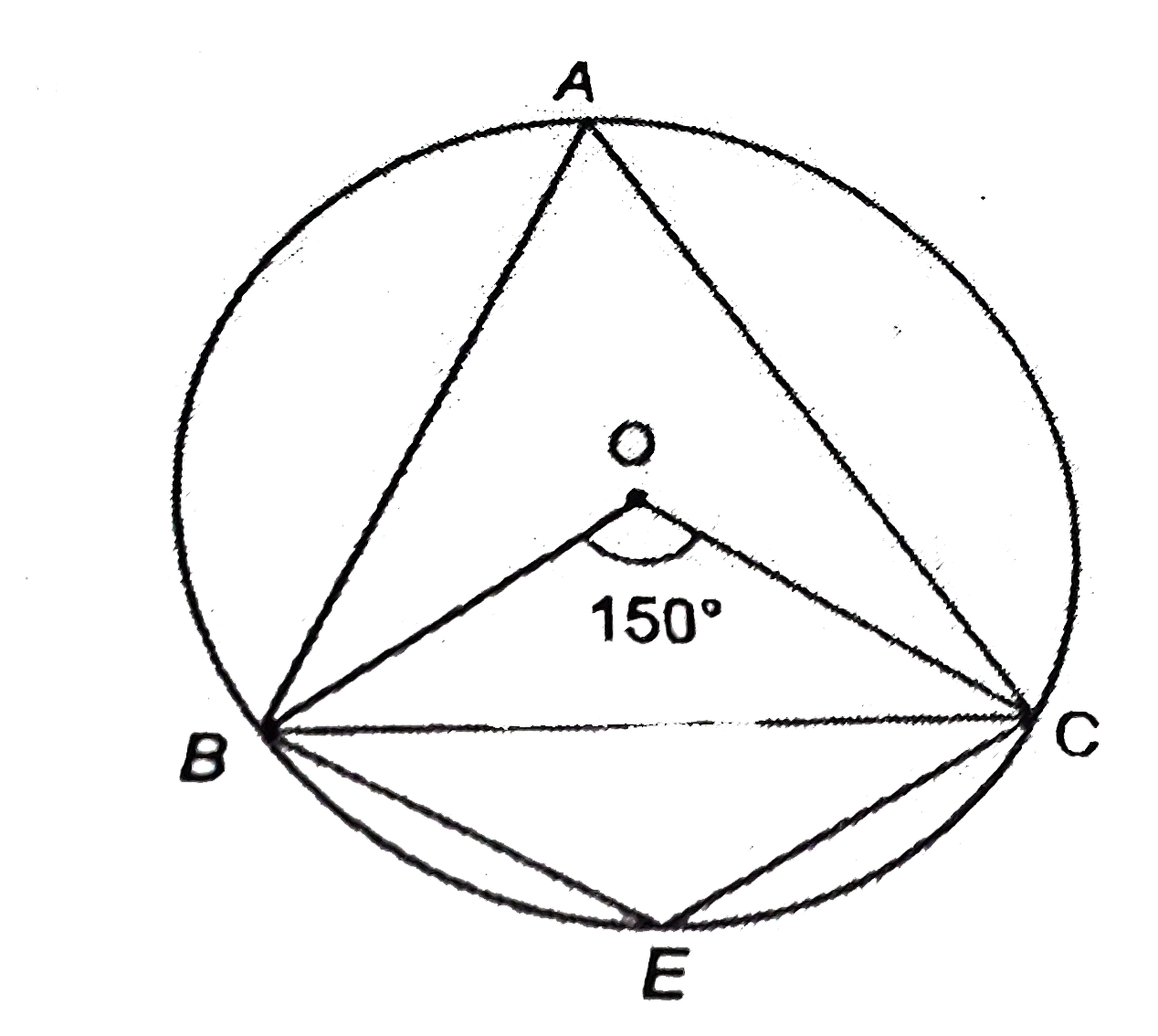 View Solution
View SolutionIn Figure, O is the centre of the circle. If ∠APB=500, find ∠AOB and ∠OAB
View SolutionIn Figure, O is the centre of the circle. If ∠BOD=1600, find the values of x and y
View Solution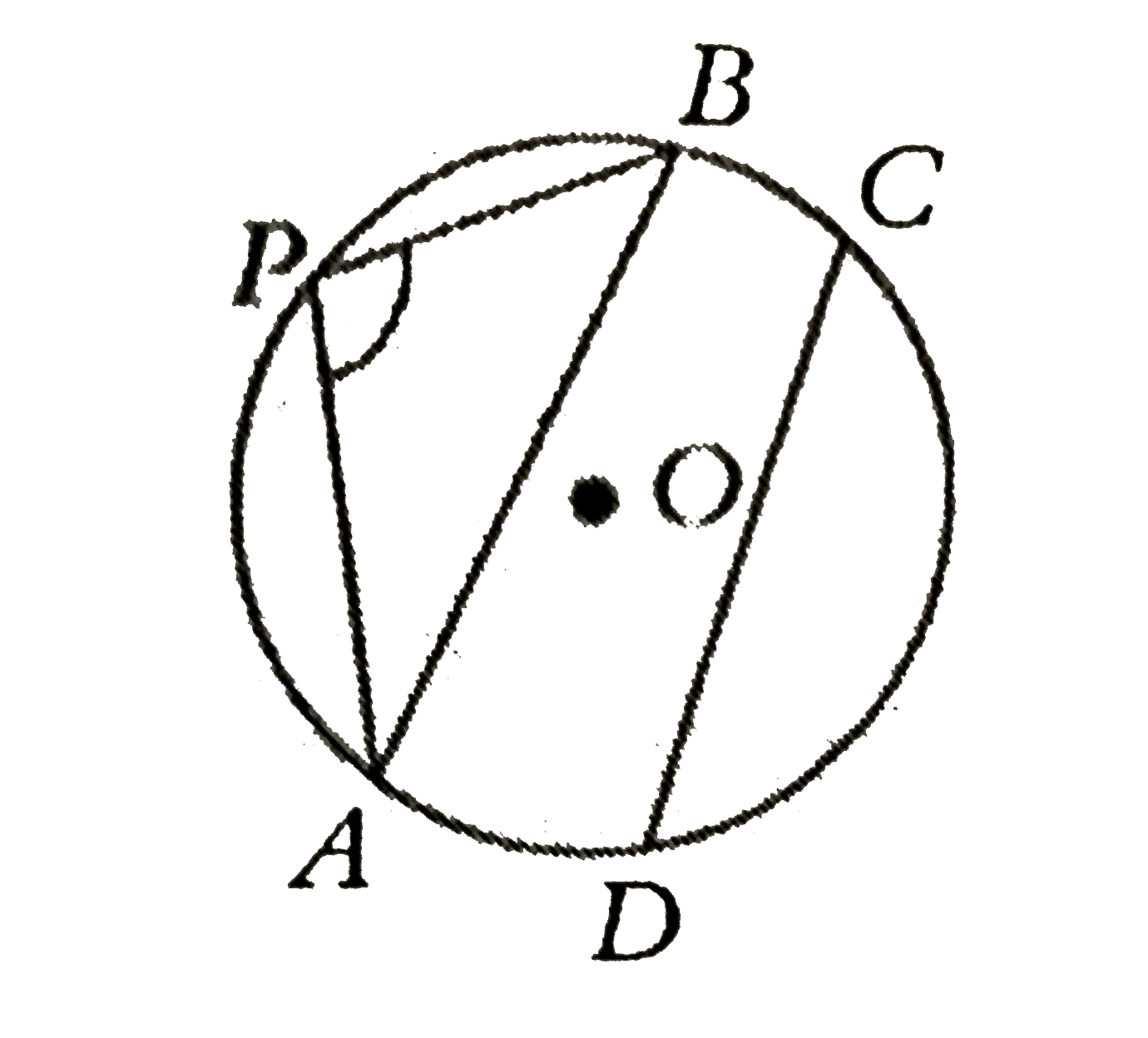
In the above figure, O is the centre of the circle and AB=CD. If ∠APB=110∘, then find the angle made by the chord CD at the centre.View Solution

