In Figure, P and Q are centres of two circles intersecting at B and C.ACD is a straight line. Then, ∠BQD=
To solve the problem step by step, we will use the properties of circles, angles at the center, and cyclic quadrilaterals.
Step 1: Understand the Given Information
We have two circles with centers P and Q that intersect at points B and C. The line ACD is a straight line. We need to find the angle ∠BQD.
Hint: Identify the centers and the points of intersection clearly.
Step 2: Identify the Angles at the Center
Given that the angle ∠APB is 1.5 times the angle ∠BQC (the angle subtended at the center is twice that subtended at the circumference), we can express this relationship mathematically.
Hint: Remember that the angle at the center is double the angle at the circumference for the same arc.
Step 3: Calculate the Angle at the Circumference
Since ∠APB = 1.5, we can find ∠BQC:
- ∠BQC = 1/2 * ∠APB = 1/2 * 1.5 = 0.75 (or 75 degrees).
Hint: Use the relationship between angles at the center and at the circumference to find the required angle.
Step 4: Identify the Cyclic Quadrilateral
Now, we consider the cyclic quadrilateral BJD (where D is a point on the line ACD). In a cyclic quadrilateral, the sum of the opposite angles is 180 degrees.
Hint: Recall the property of cyclic quadrilaterals that relates opposite angles.
Step 5: Set Up the Equation for the Cyclic Quadrilateral
Let’s denote the angle ∠BJD as x. According to the cyclic quadrilateral property:
- ∠BJC + ∠BJD = 180 degrees
- We already found ∠BJC = 75 degrees, so:
- 75 + x = 180
- x = 180 - 75 = 105 degrees.
Hint: Use the cyclic quadrilateral property to find the unknown angle.
Step 6: Relate the Angles to Find ∠BQD
Now we know that ∠BJD = 105 degrees. The angle ∠BQD is twice the angle ∠BJD because it is at the center Q:
- ∠BQD = 2 * ∠BJD = 2 * 105 = 210 degrees.
Hint: Remember that the angle at the center is double that of the angle at the circumference.
Final Answer
Thus, the angle ∠BQD = 210 degrees.
We have two circles with centers P and Q that intersect at points B and C. The line ACD is a straight line. We need to find the angle ∠BQD.
Given that the angle ∠APB is 1.5 times the angle ∠BQC (the angle subtended at the center is twice that subtended at the circumference), we can express this relationship mathematically.
Since ∠APB = 1.5, we can find ∠BQC:
- ∠BQC = 1/2 * ∠APB = 1/2 * 1.5 = 0.75 (or 75 degrees).
Now, we consider the cyclic quadrilateral BJD (where D is a point on the line ACD). In a cyclic quadrilateral, the sum of the opposite angles is 180 degrees.
Let’s denote the angle ∠BJD as x. According to the cyclic quadrilateral property:
- ∠BJC + ∠BJD = 180 degrees
- We already found ∠BJC = 75 degrees, so:
- 75 + x = 180
- x = 180 - 75 = 105 degrees.
Now we know that ∠BJD = 105 degrees. The angle ∠BQD is twice the angle ∠BJD because it is at the center Q:
- ∠BQD = 2 * ∠BJD = 2 * 105 = 210 degrees.
Thus, the angle ∠BQD = 210 degrees.
Topper's Solved these Questions
Similar Questions
In Figure, P and Q are centres of two circles intersecting at B and C.ACD is a straight line. Then, ∠BQD=
View SolutionIn Figure, XandY are the mid-points of ACandAB respectively, QP,BCandCYQandBXP are straight lines. Prove that ar(ABP)=ar(ACQ)
 View Solution
View SolutionIn Figure, AB is a diameter of the circle such that ∠A=350and ∠Q=250, find ∠PBR
View SolutionIf AB is a chord of a circle, Pand Q are the two points on the circle different from A and B, then ∠APB= ∠AQB ∠APB+∠AQB=180∘ or∠APB= ∠AQB
View SolutionIn Figure ABCDandAEFD are two parallelograms. Prove that: PE=FQ
 View Solution
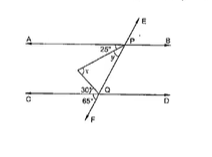
View SolutionIn Figure, AB and CD are parallel lines and transversal EF intersects them at P and Q respectively. If ∠APR=250, ∠RQC=300and ∠CQF=650, then x=550, y=440 (b) x=550, y=450 x=600, y=350 (d) x=350, y=600
 View Solution
View SolutionIn Fig.99, ABCD and EF is a transversal intersecting AB and CD at P and Q respectively. The measure of ∠DPQ is (a) (b)(c)(d)(e)100(f)0(g)(h)(i) (j) (b) (k)(l)(m)(n)80(o)0(p)(q)(r) (s) (c) (d)(e)(f)(g)110(h)0(i)(j)(k) (l) (d) (m)(n)(o)(p)70(q)0(r)(s)(t) (u)
View SolutionIn Fig.100, ABCD and EF is a transversal intersecting AB and CD at P and Q respectively. The measure of ∠DOP is (a) 65 (b) 25 (c) 115 (d) 105
View SolutionTwo circle with centres A and B intersect at C and D. Prove that ∠ACB=∠ADB.
View SolutionAB and CD are two chords of a circle such that AB=6 cm, CD=12 cm and ABCD. If the distance between AB and CD is 3 cm, find the radius of the circle.
View Solution

