Question

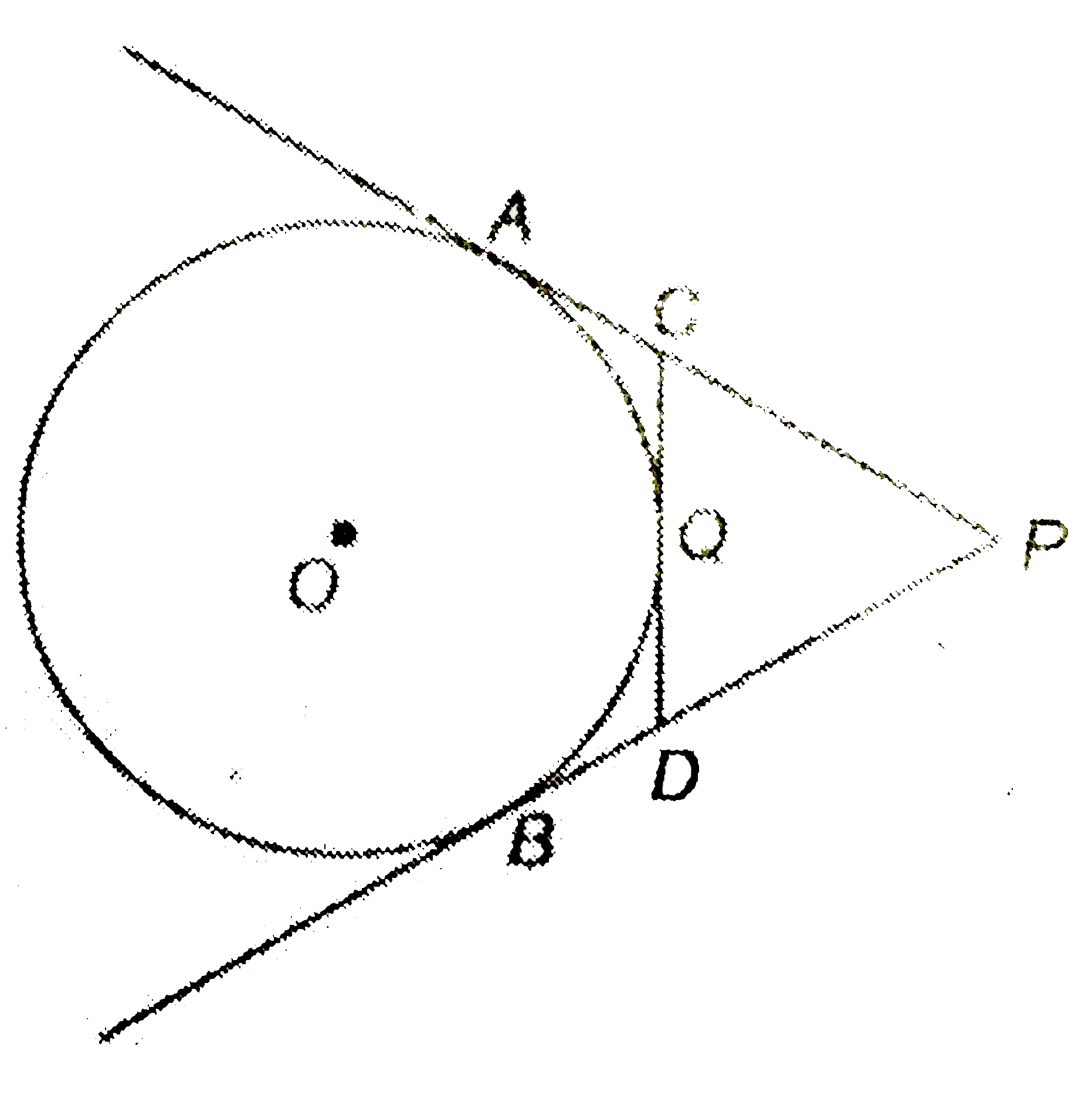
In Figure, there are two concentric circles with centre $O$
. $PR$
and $PQS$
are
tangents to the inner circle from point plying on the outer circle. If $PR=7.5cm$
, then $PS$
is equal
to
(a)
10cm (b) 12cm (c) 15cm (d) 18cm

Explanation

To solve the problem step by step, we will analyze the given information about the concentric circles and the tangents.

Step 1: Understand the Configuration
We have two concentric circles with center O. The tangents PR and PS are drawn from point P on the outer circle to the inner circle.

Step 2: Use the Property of Tangents
From the property of tangents, we know that the lengths of tangents drawn from a common external point to a circle are equal. Therefore, we can state:
\( PR = PS \)

Step 3: Identify the Given Length
We are given that:
\( PR = 7.5 \, \text{cm} \)

Step 4: Apply the Tangent Property
Since \( PR = PS \), we can substitute the value of \( PR \) into the equation:
\( PS = PR = 7.5 \, \text{cm} \)

Step 5: Find the Length of PS
Now, we need to find the total length of PS. The tangents from point P to the inner circle are equal, so we can express PS in terms of PR:
\( PS = PQ + QS \)
Where \( PQ \) is equal to \( PR \) and \( QS \) is also equal to \( PR \).

Step 6: Calculate PS
Since both \( PQ \) and \( QS \) are equal to \( PR \):
\( PS = PR + PR = 7.5 \, \text{cm} + 7.5 \, \text{cm} = 15 \, \text{cm} \)

Conclusion
Thus, the length of \( PS \) is:
\( PS = 15 \, \text{cm} \)

The correct option is (c) 15 cm.

---