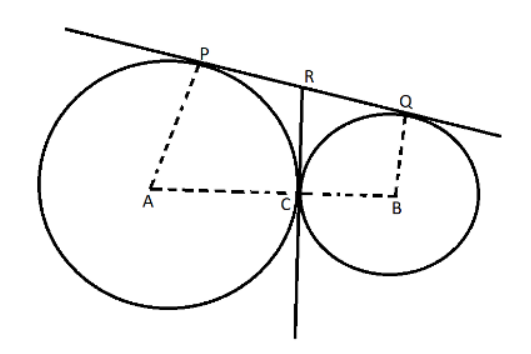
In Figure, two circles touch each other at the point C . Prove that the common tangent to the circles at C , bisects the common tangent at P and Q .
To prove that the common tangent to the circles at point C bisects the common tangent at points P and Q, we will follow these steps:
Step 1: Identify the Elements
Let the two circles be centered at points A and B, touching each other at point C. The common tangent at point C touches the first circle at point P and the second circle at point Q.
Step 2: Use the Tangent Property
According to the property of tangents, the lengths of tangents drawn from an external point to a circle are equal. Therefore, we can write:
- For circle A: PR=RC (where R is the point where the tangent touches circle A)
- For circle B: RQ=RC
Step 3: Set Up the Equations
From the above property, we can express the lengths as:
1. PR=RC (Equation 1)
2. RQ=RC (Equation 2)
Step 4: Equate the Lengths
From Equation 1 and Equation 2, we have:
- PR=RC
- RQ=RC
This implies:
- PR=RQ
Step 5: Conclusion
Since PR=RQ, it follows that point R is the midpoint of segment PQ. Therefore, the common tangent at point C bisects the segment PQ.
Final Statement
Hence, we have proved that the common tangent to the circles at point C bisects the common tangent at points P and Q.
---
Let the two circles be centered at points A and B, touching each other at point C. The common tangent at point C touches the first circle at point P and the second circle at point Q.
According to the property of tangents, the lengths of tangents drawn from an external point to a circle are equal. Therefore, we can write:
- For circle A: PR=RC (where R is the point where the tangent touches circle A)
- For circle B: RQ=RC
From the above property, we can express the lengths as:
1. PR=RC (Equation 1)
2. RQ=RC (Equation 2)
From Equation 1 and Equation 2, we have:
- PR=RC
- RQ=RC
- PR=RQ
Since PR=RQ, it follows that point R is the midpoint of segment PQ. Therefore, the common tangent at point C bisects the segment PQ.
Hence, we have proved that the common tangent to the circles at point C bisects the common tangent at points P and Q.
Topper's Solved these Questions
Similar Questions
In the figure, two circles touch each other at the point C.Prove that the common tangents to the circles at C, bisect the common tangents at P and Q.
 View Solution
View SolutionIn the given figure, two circles touch each other externally at point P. AB is the direct common tangent of these circles. Prove that:
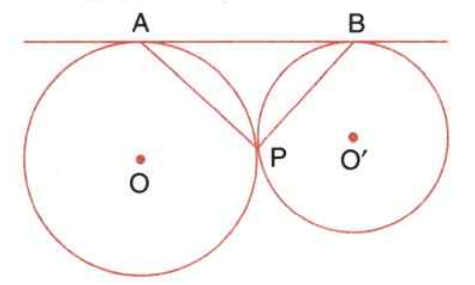
(i) tangent at point P bisects AB
(ii) angle APB=90∘View SolutionTwo circles touch each other internally. Show that the tangents drawn to the two circles from any point on the common tangent, are equal in length.
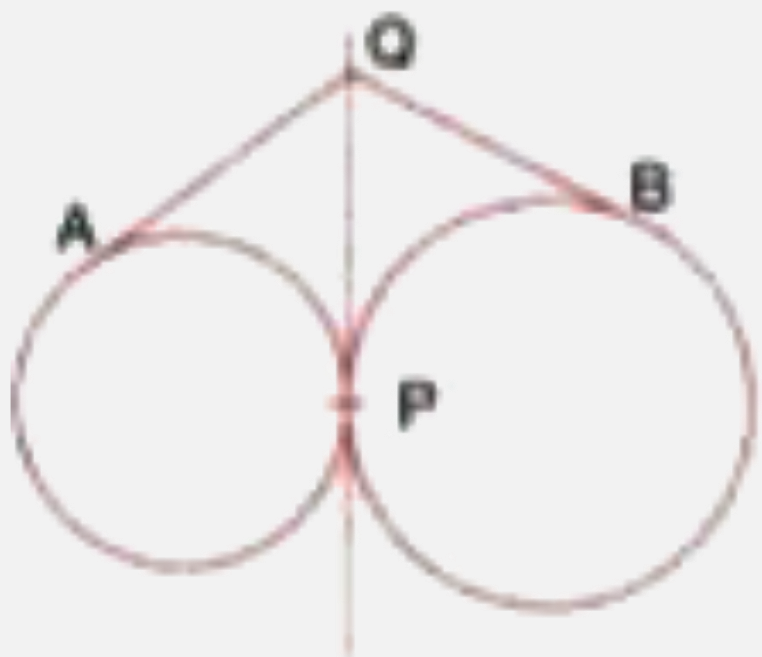
View SolutionTwo circles touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.
 View Solution
View SolutionLet P and Q be 2 circles externally touhing each other at point X. Line segment AB is a direct common tangent to circle P and Q at points A and B respectively. Another common tangent to P and Q at X intersects line AB at a point Y. If BY = 10 units and the radius of P is 9 units, then the value of the reciprocal of the radius of the radius of the circle Q is equal to
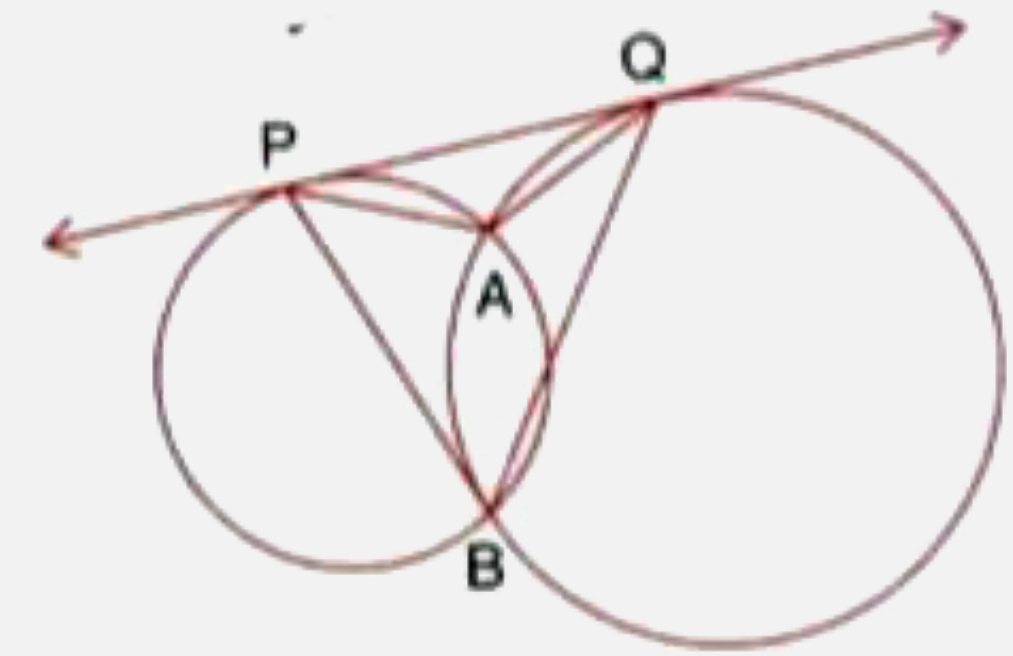
View SolutionTwo circles intersect each other at point A and B. Their common tangent touches the circles at points P and Q as shown in the figure. Show that the angles PAQ and PBQ are supplementary.
 View Solution
View SolutionTwo equal circles touch each other externally at C and AB is a common tangent to the circles. Then, ∠ACB= 60o (b) 45o (c) 30o (d) 90o
View SolutionTwo circles with centres A and B intersect each other at points P and Q. Prove that the centre-line AB bisects the common chord PQ perpendicularly.
View SolutionIn the given figure, there are two circles with centers A and B. The common tangent to the circles touches them, respectively,at P and Q. AR is 40cm and AB is divided by the point of contact of the circles in the ratio 5:3

The radius of the circle with center B isView SolutionIn Figure, two equal circles touch each other at T , if QP=4.5cm , then QR= (a) 9cm (b) 18cm (c) 15cm (d) 13.5cm
View Solution

