Question

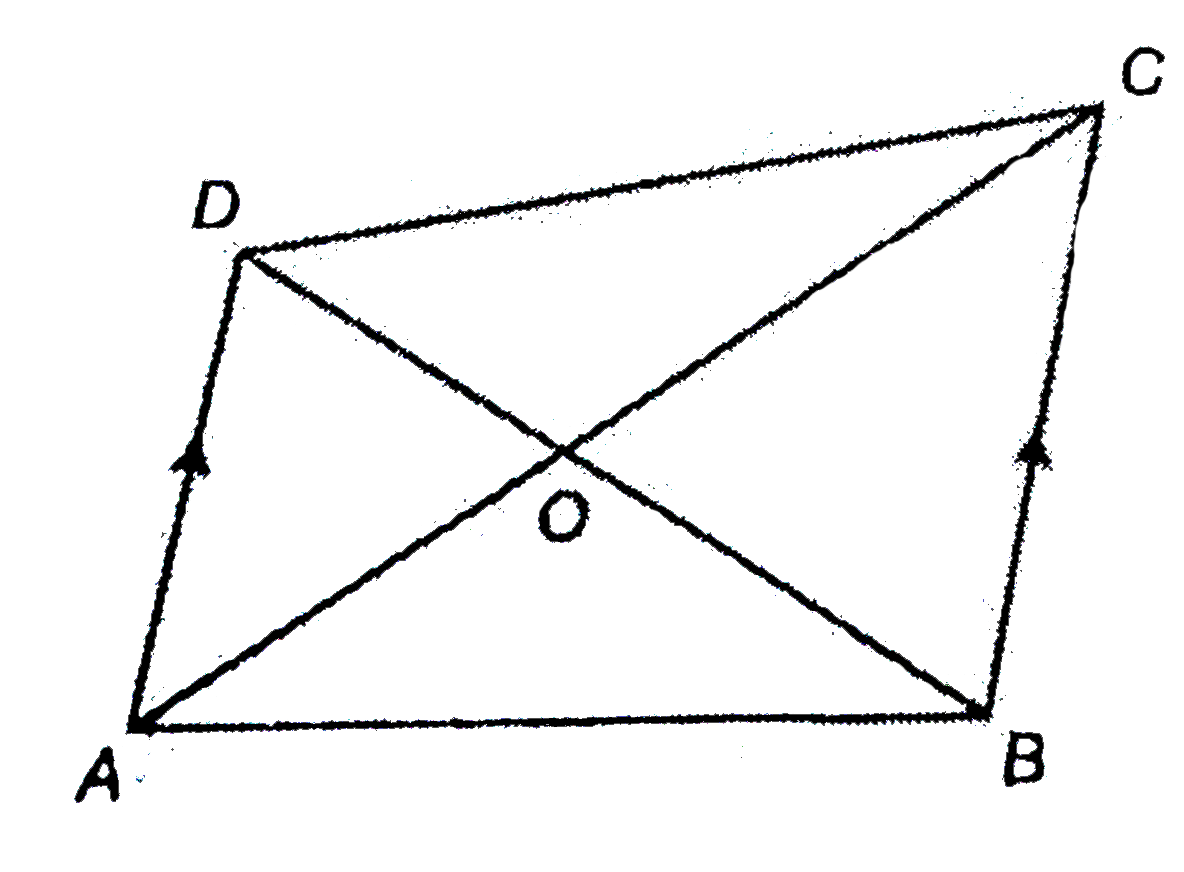
 In quadrilateral ABCD, the diagonals AC and BD intersect each other at point O.
If AO = 2CO and BO = 2DO, show that: 
$\Delta AOB$ is similar to $\Delta COD$.

Explanation

To show that triangle AOB is similar to triangle COD, we will use the given information about the segments of the diagonals and the properties of angles.

1. Identify the Given Information:
- We have quadrilateral ABCD with diagonals AC and BD intersecting at point O.
- It is given that AO = 2CO and BO = 2DO.

2. Express the Ratios:
- From AO = 2CO, we can express the ratio:
\( \frac{AO}{CO} = 2 \)
- From BO = 2DO, we can express the ratio:
\( \frac{BO}{DO} = 2 \)

3. Write the Ratios in Fraction Form:
- We can rewrite the ratios as:
\( \frac{AO}{CO} = \frac{2}{1} \quad \text{(1)} \)
\( \frac{BO}{DO} = \frac{2}{1} \quad \text{(2)} \)

4. Identify Vertically Opposite Angles:
- Since diagonals intersect, angle AOB and angle COD are vertically opposite angles. Therefore:
\( \angle AOB = \angle COD \)

5. Apply the Side-Angle-Side (SAS) Similarity Criterion:
- We have established that:
- \(\frac{AO}{CO} = 2\)
- \(\frac{BO}{DO} = 2\)
- \(\angle AOB = \angle COD\)
- According to the Side-Angle-Side (SAS) similarity criterion, if two sides of one triangle are in the same ratio as two sides of another triangle and the angles between those sides are equal, then the triangles are similar.

6. Conclude Similarity:
- Therefore, we can conclude that:
\( \triangle AOB \sim \triangle COD \)

Final Answer:
Triangle AOB is similar to triangle COD.