In reference to a circle the value of π is equal to
areacircumference
areadiameter
circumferencediameter
circumferenceradius
The correct Answer is:C
To find the value of π (pi) in reference to a circle, we will evaluate the options given and determine which one correctly represents π.
1. Evaluate Option A: Area by Circumference
- The area of a circle is given by the formula:
Area=πr2
- The circumference of a circle is given by the formula:
Circumference=2πr
- Now, if we take the ratio of the area to the circumference:
AreaCircumference=πr22πr
- Simplifying this:
=r2
- Since r2 is not equal to π, Option A is incorrect.
2. Evaluate Option B: Area by Diameter
- The diameter D of a circle is given by:
D=2r
- Taking the ratio of the area to the diameter:
AreaDiameter=πr22r
- Simplifying this:
=πr2
- Since πr2 is not equal to π, Option B is also incorrect.
3. Evaluate Option C: Circumference by Diameter
- Using the circumference and diameter:
CircumferenceDiameter=2πr2r
- Simplifying this:
=π
- Since this is equal to π, Option C is correct.
4. Evaluate Option D: Circumference by Radius
- Taking the ratio of circumference to radius:
CircumferenceRadius=2πrr
- Simplifying this:
=2π
- Since 2π is not equal to π, Option D is incorrect.
Conclusion:
The correct answer is Option C: Circumference by Diameter, which equals π.
- The area of a circle is given by the formula:
Area=πr2
- The circumference of a circle is given by the formula:
Circumference=2πr
- Now, if we take the ratio of the area to the circumference:
AreaCircumference=πr22πr
- Simplifying this:
=r2
- Since r2 is not equal to π, Option A is incorrect.
- The diameter D of a circle is given by:
D=2r
- Taking the ratio of the area to the diameter:
AreaDiameter=πr22r
- Simplifying this:
=πr2
- Since πr2 is not equal to π, Option B is also incorrect.
- Using the circumference and diameter:
CircumferenceDiameter=2πr2r
- Simplifying this:
=π
- Since this is equal to π, Option C is correct.
- Taking the ratio of circumference to radius:
CircumferenceRadius=2πrr
- Simplifying this:
=2π
- Since 2π is not equal to π, Option D is incorrect.
The correct answer is Option C: Circumference by Diameter, which equals π.
Topper's Solved these Questions
- PERIMETER AND AREABOOK - NCERT EXEMPLARCHAPTER - PERIMETER AND AREAEXERCISE - Exercise (Fill in the blanks)
19 Videos
- PERIMETER AND AREABOOK - NCERT EXEMPLARCHAPTER - PERIMETER AND AREAEXERCISE - Exercise (True or false)
7 Videos
- PERIMETER AND AREABOOK - NCERT EXEMPLARCHAPTER - PERIMETER AND AREAEXERCISE - Think and Discuss
7 Videos
- LINES AND ANGLES BOOK - NCERT EXEMPLARCHAPTER - LINES AND ANGLES EXERCISE - Exercise (fill in the blanks)
3 Videos
- PRACTICAL GEOMETRY SYMMETRY AND VISUALISING SOLID SHAPESBOOK - NCERT EXEMPLARCHAPTER - PRACTICAL GEOMETRY SYMMETRY AND VISUALISING SOLID SHAPESEXERCISE - EXERCISE
108 Videos
Similar Questions
Knowledge Check
In given circle value of θ is equal to
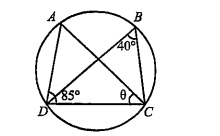 A35∘B45∘C55∘D65∘
A35∘B45∘C55∘D65∘The perimeter of an equilateral triangle is equal to the circumference of a circle. The ratio of their areas is
(Use π=227)A22:21√3B21:22√3C21:22√2D22:21√2
If the value of limx→π6cos(x+π3)(1−√3tanx) is equal to λ, then the value of 120λ2 is equal to
View Solutioninside the circles x2+y2=1 there are three circles of equal radius a tangent to each other and to s the value of a equals to
View SolutionState whether the statements are true (T) or false (F).
Ratio of area of a circle to the area of a square whose side equals radius of circle is 1:π.
View SolutionIf the area of a sector of a circle bounded by an arc of length 5π cm is equal to 20π cm2 , then the radius of the circle is (a) 12 cm (b) 16 cm (c) 8 cm (d) 10 cm
View SolutionIf cosAsin(A−π6) is maximum , when the value of A is equal to πλ, then the value of λ is
View SolutionCircumference 'C' of a circle is equal to 2π× _______.
View Solution

