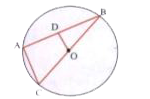
In the above diagram, BC is diameter, O is centre and OD⊥AB. If AC=λOD, then value of λ is
2
3
1
12
The correct Answer is:A
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES6videos
CIRCLES
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - TEST YOURSELF (LEVEL 3)8videos
CIRCLES
- BOOK - CENGAGECHAPTER - ALGEBRAIC EXPRESSIONS AND POLYNOMIALS EXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES10videos
ALGEBRAIC EXPRESSIONS AND POLYNOMIALS
- BOOK - CENGAGECHAPTER - LAWS OF EXPONENTS AND LOGARITHMS EXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES10videos
LAWS OF EXPONENTS AND LOGARITHMS
Similar Questions
Knowledge Check
- Question 1 - Select One
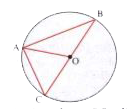
In the above figure, BC is diameter and O is centre. If area (ΔOAB)=k× area (ΔOAC) then K isA√2B12C1D2 - Question 2 - Select One
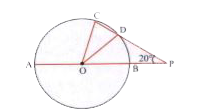
In the above figure, AB is diameter with length 2x. If ∠APC=20∘andOD=DP, where O is the centre, then length of AC isAx3B2xCx2Dx - Question 3 - Select One
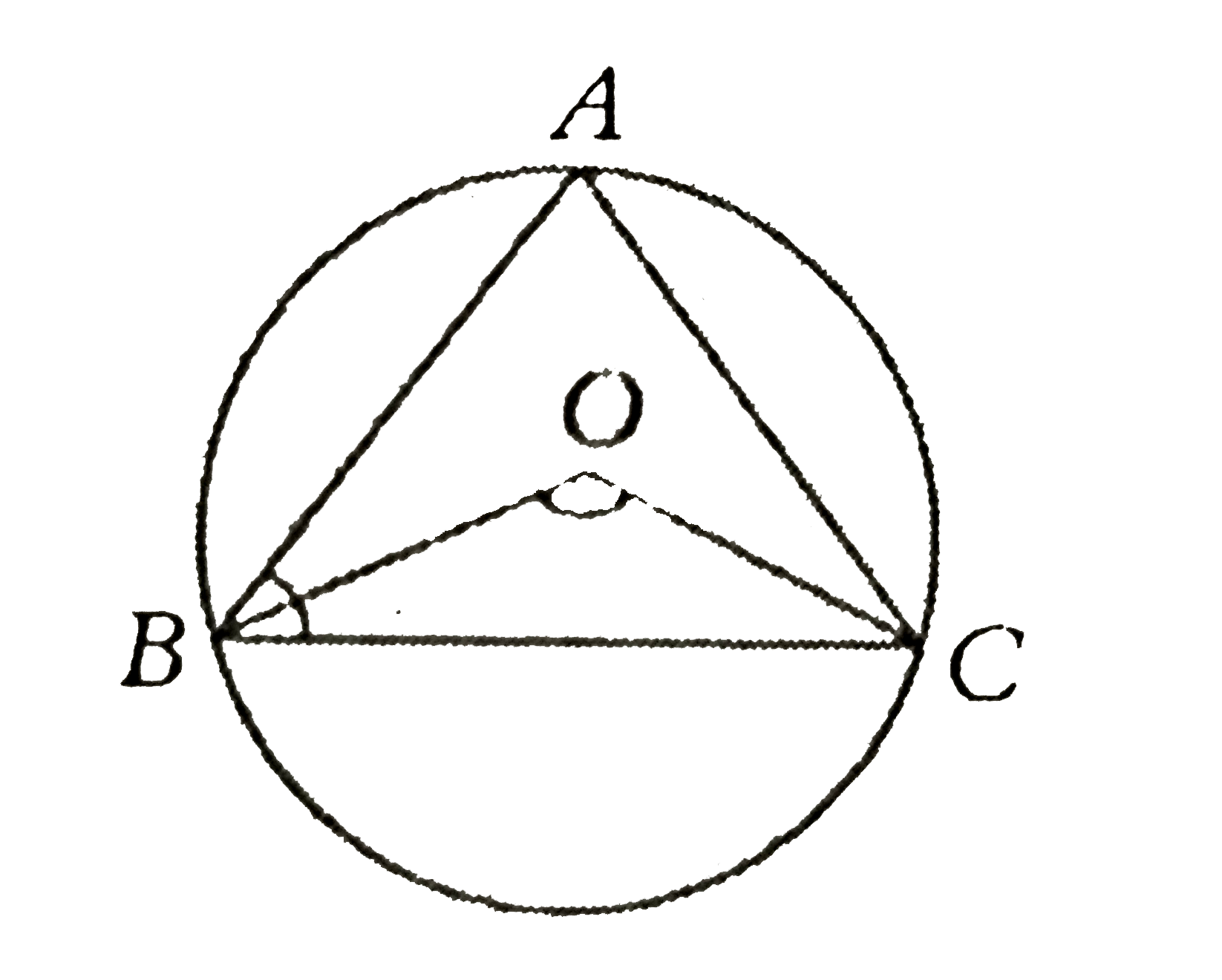
In the above diagram (not to scale), AB=AC=. O is the centre of the circle. If ∠ABC=80∘, then ∠BOC=A20∘B40∘C60∘D80∘
If O is a circumcentre of ΔABC and OD⊥BC the find ∠BOD?
View SolutionIn the given figure AB is the diameter of a circle with centre O . If chord AC = chord AD, prove that :
(i) are BC=areDB
(ii) AB is bisector of ∠CAD.
Further, if the length of are AC is twice the length of are BC , find :
(i) ∠BAC
(ii) ∠ABC View Solution
View Solution
In the figure above (not to scale), AB is the diameter of the circle with centre O. If ∠ACO=30∘, then find ∠BOC.View SolutionIn the given figure, O is the centre of the bigger circle and AC is its diameter. Another circle with AB as diameter is drawn. If AC = 54 cm and BC = 10 cm. Find the area of the shaded region
 View Solution
View SolutionIn the given figure, O is the centre of the bigger circle and AC is its diameter. Another circle with AB as diameter is drawn. If AC = 54 cm and BC = 10 cm. Find the area of the shaded region
 View Solution
View Solution

