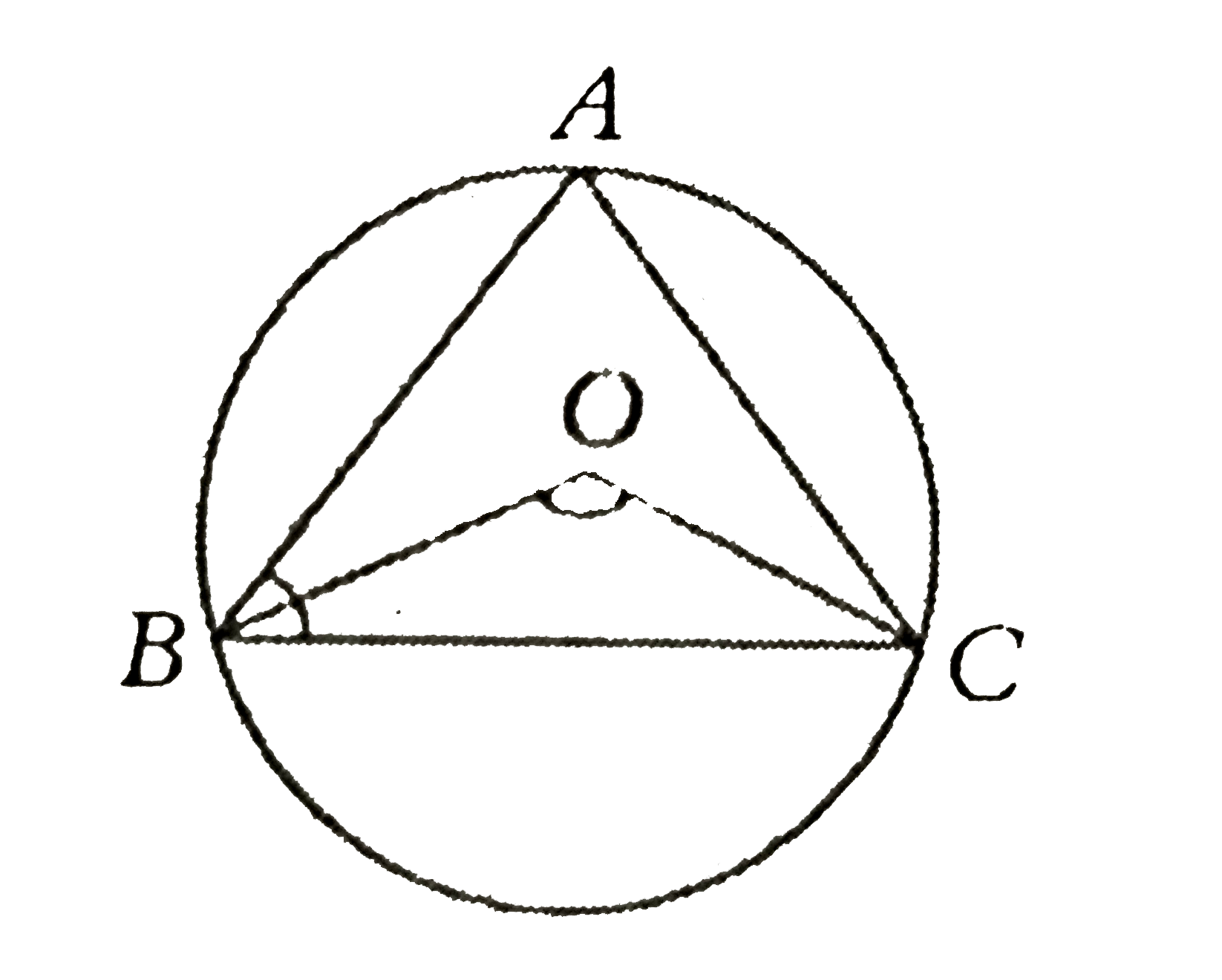
In the above diagram (not to scale), AB=AC=. O is the centre of the circle. If ∠ABC=80∘, then ∠BOC=
20∘
40∘
60∘
80∘
The correct Answer is:b
(i) Angle subtended by a chord at the centre of a circle is twice the angle subtended by it at any point on he circumference in the same segment in which the centre lies.
(ii) ABC is an isosceles triangle, i.e.,∠ABC=∠BCA, using this find ∠BAC.
(iii) Then use the property that angle made by an arc at the centre of the circle is double the angle made by the same arc at any point on the remaining part of the circle.
Topper's Solved these Questions
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Level 2
20 Videos
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Level 3
7 Videos
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Essay type Question
3 Videos
- FormulaeBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FormulaeEXERCISE - Level 3
7 Videos
- INDICESBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - INDICESEXERCISE - CONCEPT APPLICATION (Level 3)
7 Videos
Similar Questions
Knowledge Check
-
In the above diagram (not to scale), AB=AC=. O is the centre of the circle. If ∠ABC=80∘, then ∠BOC=A20∘B40∘C60∘D80∘
In the figure O is the centre of the circle and ∠POR=80∘.Then ∠RQS is
View Solution
In the figure (not to scale ), O is the centre of the circle and ∠OBA=30∘. Find ∠ACB
View Solution
In the above figure (not to scale), O is the centre of the circle AC and OB are parallel lines .If ∠ACO=80∘ , then find ∠ADO .
View SolutionIn the figure, O is the centre of the circle such that ∠AOC−140∘, then ∠ABC=…….
View Solution
In the figure above (not to scale), AB is the diameter of the circle with centre O. If ∠ACO=30∘, then find ∠BOC.
View SolutionIn the given figure, O is the centre of the circle and BA = AC. If ∠ABC=50∘, find ∠BOC and ∠BDC.
View Solution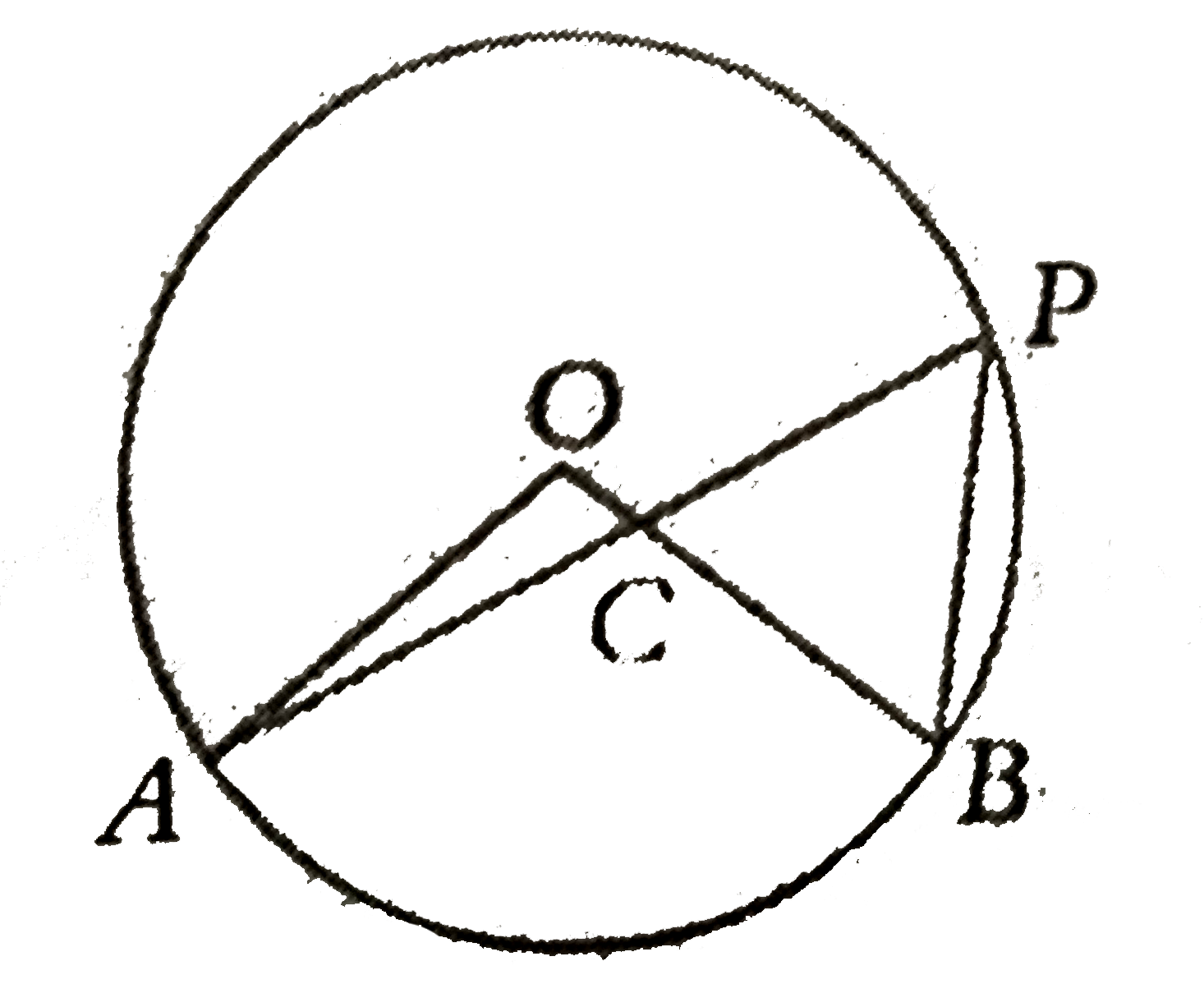
In the above figure (not to scale), O is the centre of the circle. ¯¯¯¯¯¯AP and ¯¯¯¯¯¯BP are two chords. C is the point of intersection of ¯¯¯¯¯¯AP and ¯¯¯¯¯¯OB. If ∠OAC=30∘ and ∠PBC=80∘, then ∠AOB=
View Solution