In the adjoining figure, AB and AC are two equal chords of a circle with centre O . Show that O lies on the bisector of ∠BAC.
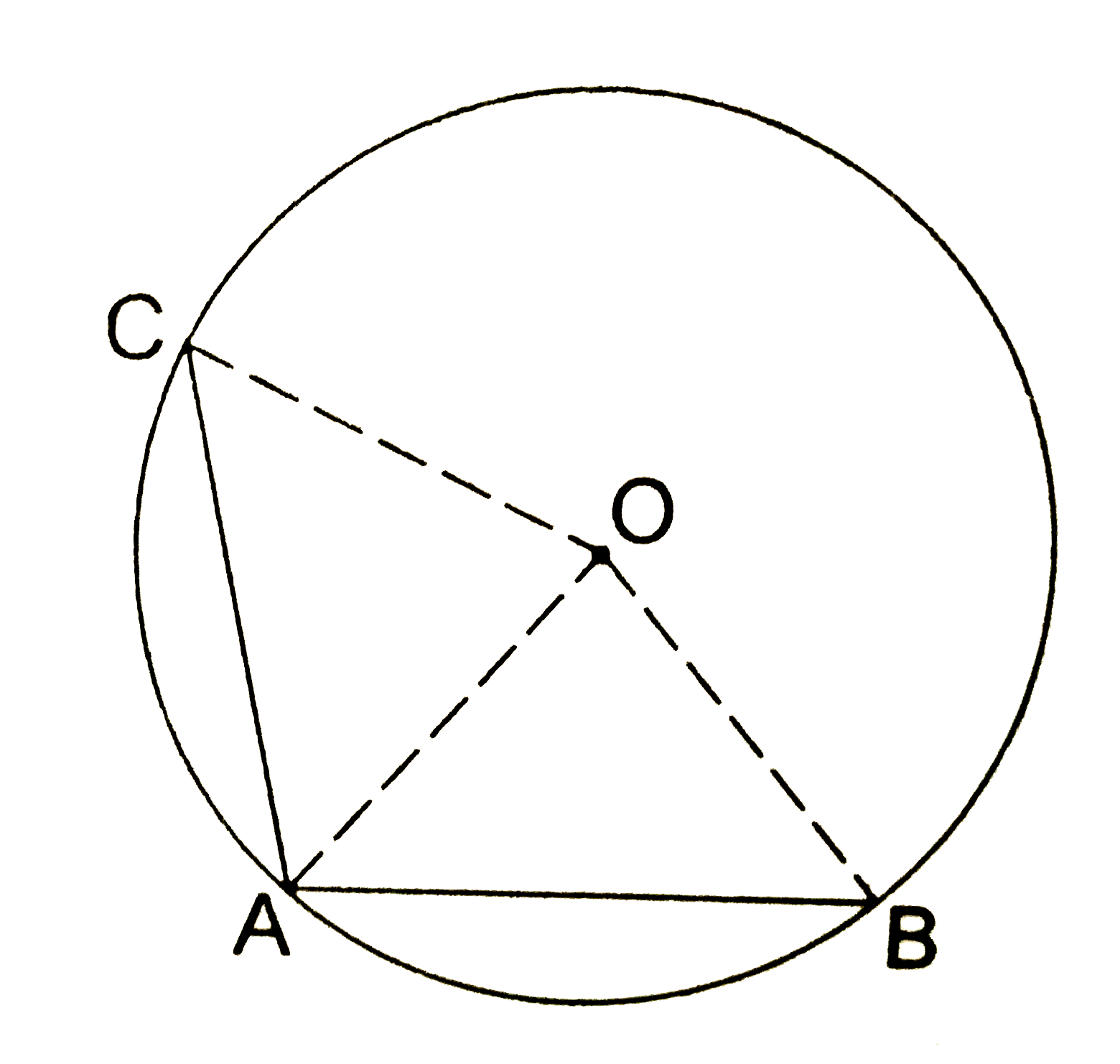
Join OA,OB and OC
ΔOAB≅ΔOAC[∵OA=OA,OB=OC=r,AB=AC]
⇒∠OAB=∠OAC
Similar Questions
Knowledge Check
AB and AC are tangents to the circle with centre O. Then x equals.
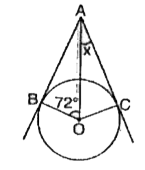 A22∘B18∘C20∘D36∘
A22∘B18∘C20∘D36∘
In the given figure,AB and CDare equal chords of a circle with centre O .Prove that ∠AOB≅∠COD and ∠AOB=∠COD
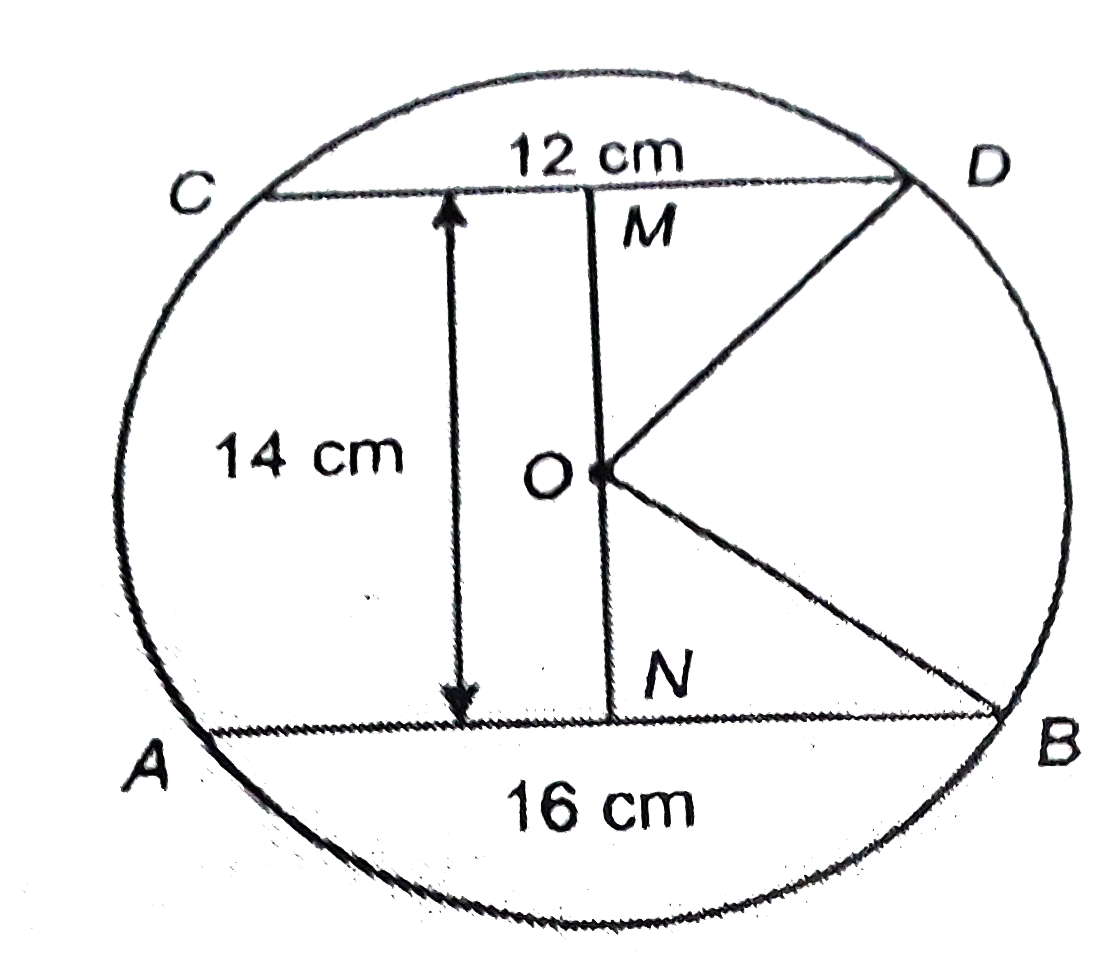
View SolutionIn the adjoining figure ,AB and CD are two parallel chords of a circle with centre O , whose length are 16 cm and 12 cm respectively. Find the radius of the circle if the distance between them is 14 cm.
View SolutionAB and CD are equal and parallel chords of a circle with centre O. Then AC passes through the centre O. [Agree / Disagree]
View SolutionIn the given figure, AB and CD are two equal chords. If O is the centre of the circle , ∠AOB=120∘, then find ∠OCD.

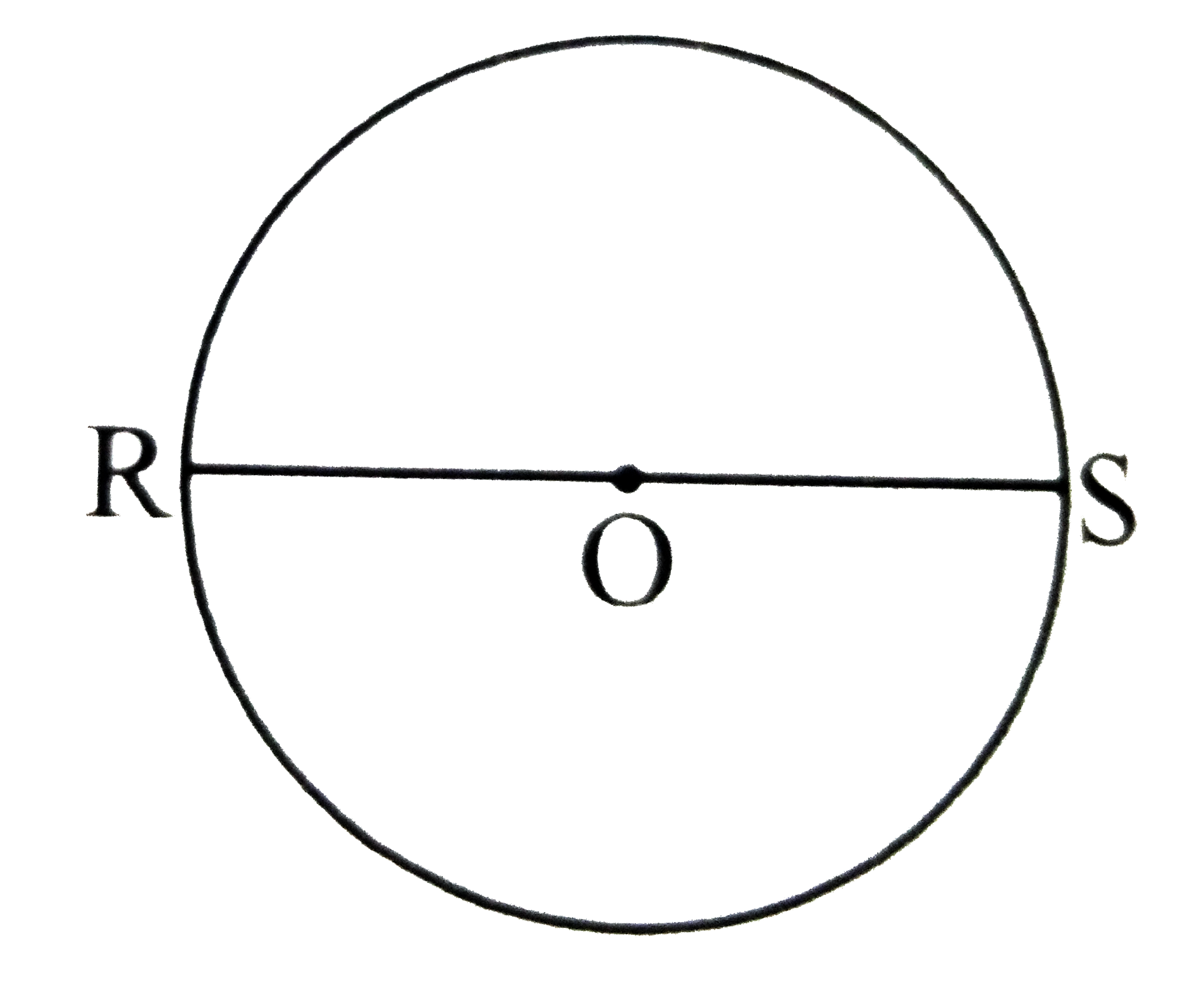
View SolutionIn the adjoining figure, seg RS is a diameter of the circle with centre O. Point T lies in the exterior of the circle. Prove that ∠RTS is an acute angle.
View SolutionIf two chords AB and AC of a circle with centre O are such that the centre O lies on the bisector of ∠BAC, prove that AB=AC , i.e. the chords are equal.
View SolutionTwo chord AB and AC of a circle are equal. Prove that the centre of a circle lies on the angle bisector of ∠BAC
View Solution
