In the adjoining figure, ABCD is a parallelogram and E is the midpoint of AD. A line through D, drawn parallel to EB, meets AB produced at F and BC at L. Prove that
(i) AF = 2 DC and (ii) DF = 2DL.
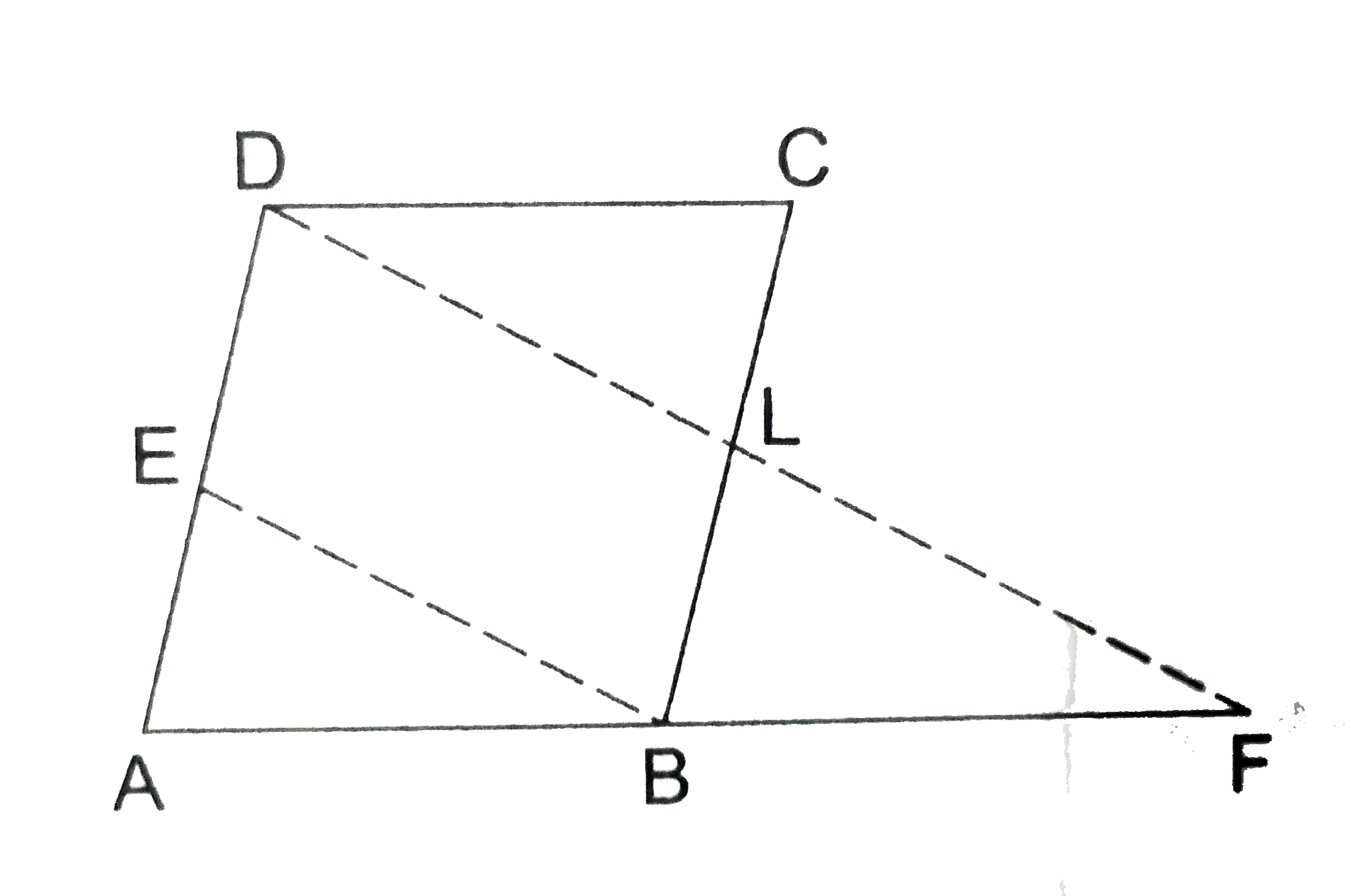
EB|| DL and ED ||BL ⇒ EBLD is a ||gm.
∴BL=ED=12AD=12BC=CL.
Now, in △DCL and FBL, we have
CL= BL (proved), ∠DLC=∠FLB (vert. opp. ∠)
and∠CDL=∠BFL (alt. int. ∠).
∴△DCL≅△FBL.
∴DC=BFandDL=FL.
Now, BF=DC=AB⇒2AB=2DC⇒AF=2DC.
DL=FL⇒DF=2DL.
Topper's Solved these Questions
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Exercise 10 A
10 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - EXERCISE 10B
27 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Matching of Columns:
2 Videos
- PROBABILITYBOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
10 Videos
Similar Questions
Knowledge Check
ABCD is a parallelogram and L is a point on DB . The produced line AL meets BC at M and DC produced at N .
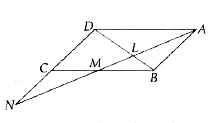
Given that DL =3LB , find ABCN .A3/2B1/2C4/5D1/4
In the given figure, ABCD is a parallelogram and E is the midpoint of side BC. If DE and AB when produced meet at F, prove that AF = 2AB.

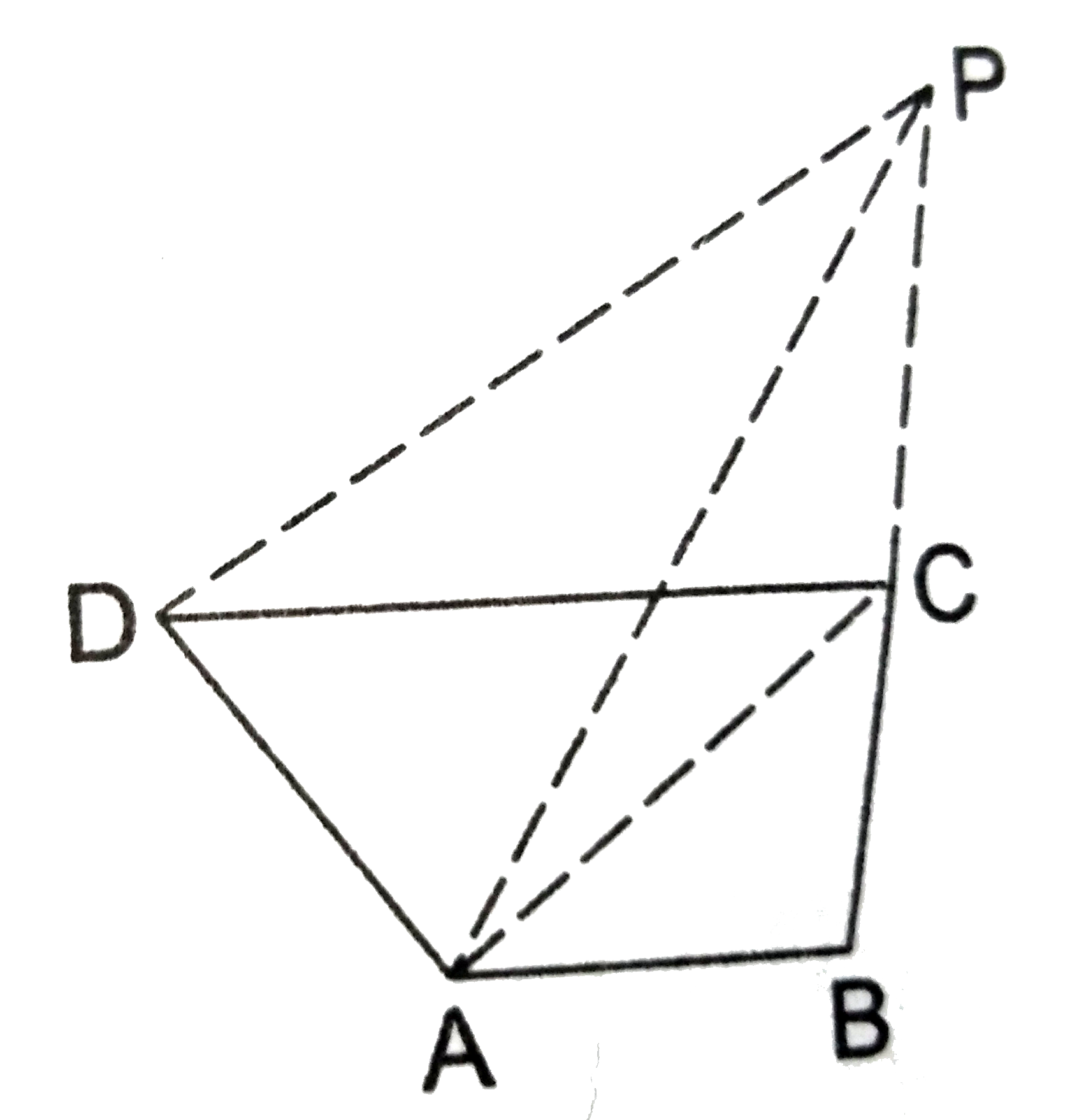
View SolutionIn the adjoining figure, ABCD is a quadrilateral. A line through D, parallel to AC, meets BC produced in P .
Prove that ar(△ABP)=ar(qaud. ABCD).
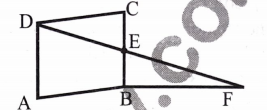
View SolutionIn the given figure, ABCD is a ||gm and E is the mid-point of BC. Also, DE and AB when produced meet at F. Then.
View SolutionP is the mid-point of side AB of a parallelogram ABCD . A Line through B parallel to PD meets DC at Q and AD produced at R . Prove that (i) AR=2BC (ii) BR=2BQ.
View SolutionP is the mid-point of side AB of parallelogram ABCD. A line drawn from B parallel to PD meets CD at Q and AD produce at R. Prove that :
(i) AR = 2BC (ii) BR= 2BQ
View SolutionAB and CD are the parallel sides of a trapeziuml. E is the mid-point of AD. A line through E and parallel to side AB meets the line BC at point F. Prove that F is the mid-point of BC.
View SolutionIn the figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that

ar(ΔAEDF) = ar(ΔABCDE)
View Solution

