In the adjoining figure. If two equal chords AB and CD of a circle intersect each other at E. then prove that chords AC and DB are equal.

We have, ⇒
⌢AB≅⌢CD (if two chords of a circle are equal then their corresponding arcs are congruent)
Subtracting ⌢CB from both sides,we get
⌢AB−⌢CB≅⌢CD−⌢CB
⇒⌢AC≅⌢DB
⇒AC=DB (if two arcs are congruent then their corresponding chords are equal).
Similar Questions
In the figure, two equal chords AB and CD of a circle with centre O, intersect each other at E, Prove that AD=CB
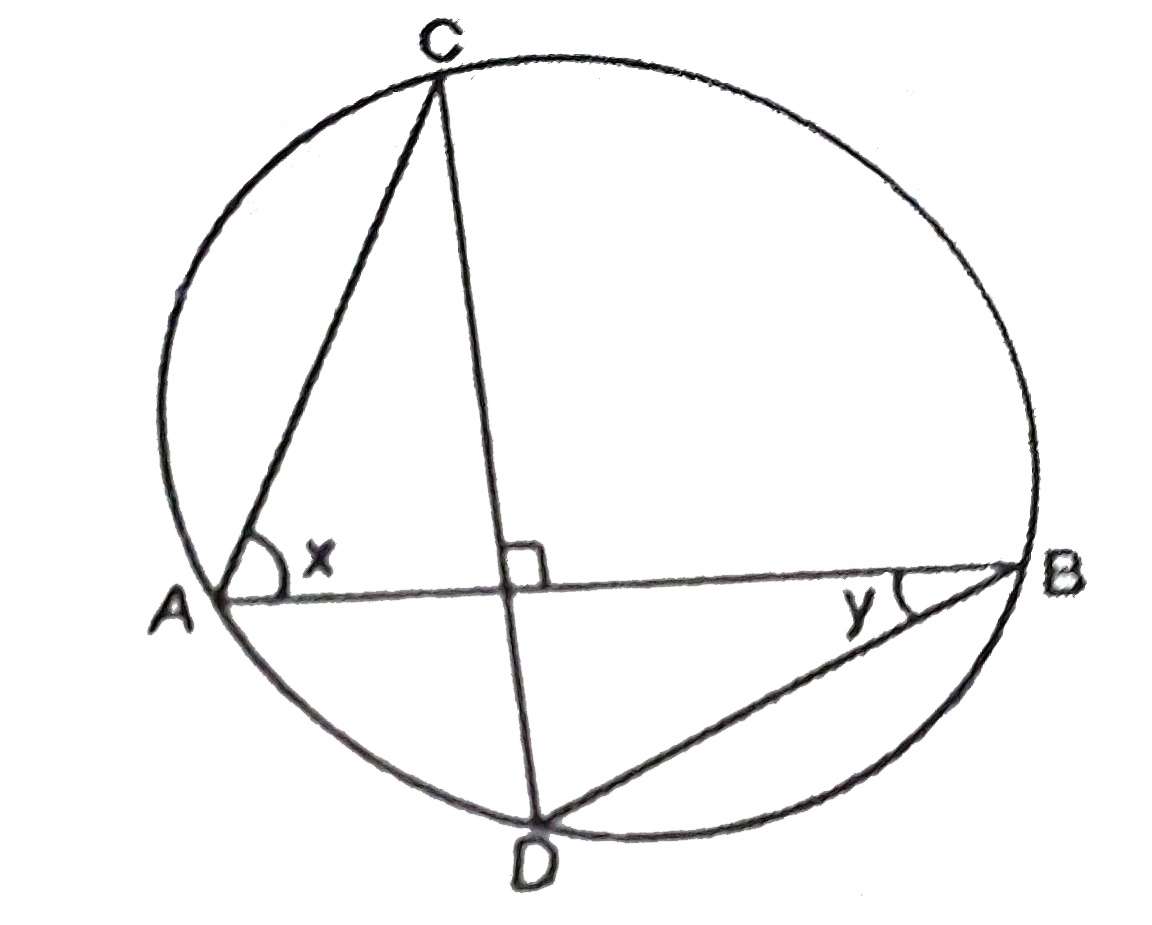
View SolutionIn the adjoining figure, if chords AB and CD of the circle intesect each other at right angles, then find the value of x+y.
View SolutionIf chords AB and CD of a circle intersect each other at a point inside the circle, prove that : PA×PB=PC×PD .
View SolutionIn the adjoining figure, common tangents AB and CD to two circles intersect at P.
Prove that AB=CD.

View SolutionTwo equal chord AB and CD of a circle with centre O, intersect each other at point P inside the circle.

Prove that:
BP=DP
View SolutionIn Figure two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that
(i) ΔPAC~ΔPDB
(ii) PA⋅PB = PC⋅PD

View SolutionTwo chords AB and CD of a circle are each at distances 4 cm from the centre. Then,
View SolutionIn figure, common tangents AB and CD to two circles intersect at E. Prove that AB=CD.

View SolutionIn Figure, two chords AB and CD intersect each other at the point P. Prove that:
(i) ΔAPC~ΔDPB
(ii) AP⋅PB=CP⋅DP

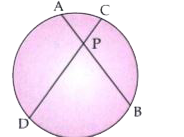
View SolutionAB and CD are two chords of a circle intersecting at P. Prove that AP×PB=CP×PD
View Solution
