In the adjoining figure, O is the centre of a circle. If AB and AC are chords of the circle such that AB =AC ,OP⊥AB and OQ⊥AC, prove that PB=QC.

Video Solution
Text Solution
AB=AC⇒12AB=12AC⇒MB=NC.
Also, ∠PMB=∠QNC=90∘
Equal chords are equidistant from the centre ⇒OM=ON.
Also, OP=OQ= radius ⇒OP−OM=OQ−ON⇒PM=QN
∴ΔMPB≅ΔDQC⇒PB=QC
|
Similar Questions
Knowledge Check
In the given figure,BD passes through centre O,AB=12 and AC=8.What is the radius of the circle?
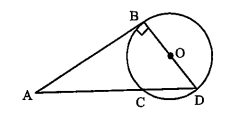 A3√2B4sqrt3C3√5D3√3
A3√2B4sqrt3C3√5D3√3In the given figure,BD passes through centre O,AB=12 and AC=8.What is the radius of the circle?
 A3√2B4√3C3√5D3√3
A3√2B4√3C3√5D3√3In the given figure, BD passes through centre O, AB = 12 and AC = 8. What is the radius of the circle?
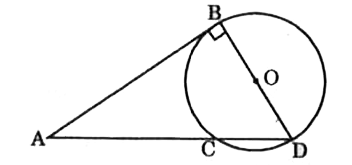 A3√2B4√3C3√5D3√3
A3√2B4√3C3√5D3√3
In the adjoining figure, O is the centre of the circle. Seg AB, seg AC are tangent segments. Radius of the circle is r and l(AB)=r. Prove that , □ ABOC is a square.
View SolutionIn the adjoining figure, O is the centre of the circle. If the chord AB is equal to the radius of the circle, then find the value of ∠ADB.

View SolutionIn the adjoining figure, O is the centre of a circle in which AB and CD are two diameters. Prove that AC| |BD and AD| |BC. If ∠OBD=50∘, then find the value of ∠AOC.

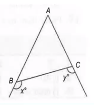
View SolutionIn the adjoining figure, x>y, Prove that AB>AC
View SolutionIn the adjoining figure, O is the centre of the circle and AB is its diameter. If AC=8 cm and BC= 6cm, then find the radius of the circle.

View Solution