In the figure, ABCDE is a pentagon with BE∣∣CD and BC∣∣DE. BC is perpendicular to CD. AB= 5cm, AE=5cm, BE= 7cm, BC= x-y and CD= x+y. If the perimeter of ABCDE is 27cm. find the value of x and y, given x,y,≠0
To solve the problem, we will follow these steps:
Step 1: Understand the given information
We have a pentagon ABCDE with the following dimensions:
- AB = 5 cm
- AE = 5 cm
- BE = 7 cm
- BC = x - y
- CD = x + y
- The perimeter of ABCDE is 27 cm.
Step 2: Set up the perimeter equation
The perimeter of the pentagon ABCDE can be expressed as the sum of all its sides:
Perimeter=AB+BC+CD+DE+AE
Substituting the known values:
27=5+(x−y)+(x+y)+(x−y)+5
Step 3: Simplify the perimeter equation
Now, simplify the equation:
27=5+5+(x−y)+(x+y)+(x−y)
27=10+3x−y
Now, isolate the terms involving x and y:
27−10=3x−y
17=3x−y(Equation 1)
Step 4: Set up the parallel sides equation
Since BE || CD and BC || DE, we have:
- BE = CD = 7 cm (since BE is parallel to CD)
- Therefore, we can set up the equation:
x+y=7(Equation 2)
Step 5: Solve the system of equations
Now we have two equations:
1. 3x−y=17 (Equation 1)
2. x+y=7 (Equation 2)
We can solve these equations simultaneously. From Equation 2, we can express y in terms of x:
y=7−x
Step 6: Substitute y in Equation 1
Substituting y in Equation 1:
3x−(7−x)=17
3x−7+x=17
4x−7=17
4x=24
x=6
Step 7: Find the value of y
Now substitute x=6 back into Equation 2 to find y:
6+y=7
y=1
Conclusion
Thus, the values of x and y are:
- x=6
- y=1
We have a pentagon ABCDE with the following dimensions:
- AB = 5 cm
- AE = 5 cm
- BE = 7 cm
- BC = x - y
- CD = x + y
- The perimeter of ABCDE is 27 cm.
The perimeter of the pentagon ABCDE can be expressed as the sum of all its sides:
Perimeter=AB+BC+CD+DE+AE
Substituting the known values:
27=5+(x−y)+(x+y)+(x−y)+5
Now, simplify the equation:
27=5+5+(x−y)+(x+y)+(x−y)
27=10+3x−y
Now, isolate the terms involving x and y:
27−10=3x−y
17=3x−y(Equation 1)
Since BE || CD and BC || DE, we have:
- BE = CD = 7 cm (since BE is parallel to CD)
- Therefore, we can set up the equation:
x+y=7(Equation 2)
Now we have two equations:
1. 3x−y=17 (Equation 1)
2. x+y=7 (Equation 2)
y=7−x
Substituting y in Equation 1:
3x−(7−x)=17
3x−7+x=17
4x−7=17
4x=24
x=6
Now substitute x=6 back into Equation 2 to find y:
6+y=7
y=1
Thus, the values of x and y are:
- x=6
- y=1
Topper's Solved these Questions
- SAMPLE PAPER 2019BOOK - X BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION-A (FILL IN THE BLANKS)
3 Videos
- SAMPLE PAPER 2019BOOK - X BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION-A (FILL IN THE BLANKS) 12 (a)
1 Videos
- SAMPLE PAPER 2019BOOK - X BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - 12B
1 Videos
- CBSE BOARDS 2020BOOK - X BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - CBSE BOARDS 2020EXERCISE - QUESTION
41 Videos
- X BoardsBOOK - X BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - X BoardsEXERCISE - All Questions
481 Videos
Similar Questions
ABCD is a parallelogram where DE is perpendicular to AB. If BD= 17 cm, AE = 15 cm, and area of ΔADE=60sq. cm, find the perimeter of ABCD.

View SolutionIn the given figure, AB||CDandBC||AD. Find the values of x, y and z

View SolutionIn figure, ABCD is a parallelogram, AE perpendicular to DC and CF perpendicular to AD. If AB = 16cm, AE = 8cm and CF = 10cm, Find AD.
View Solution∆ABC ~ ∆DEF. If AB = 4 cm, BC = 3.5 cm, CA = 2.5 cm and DF = 7.5 cm, find the perimeter of ∆DEF
View SolutionIn the adjoining figure AB||CD, find x and y

View SolutionIn the following figure, AE//BC. Find values of x and y.
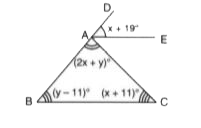
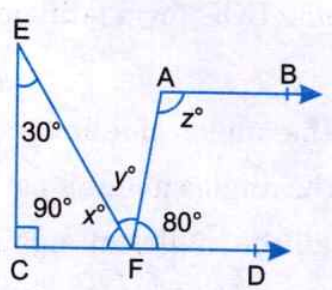
View SolutionIn the given figure, AB∣∣CD. Find the angles x, y and z
View SolutionIn parallelogram ABCD , AB = (3x- 4) cm, BC = ( y- 1) cm , CD = ( y+ 5) cm and AD = (2x+ 5) cm. find the ratio AB : BC.
Find the values of x and y.
View SolutionThe perimeter of a parallelogram ABCD = 40 cm , AB = 3x cm, BC = 2x cm and CD = 2( y+1) cm . Find the values of x and y.
View SolutionABCD is a trapezium such that AB and DC are parallel and BC is perpendicular to them. If BC=1 cm, CD=2 cm and ∠ADB=45∘, then the lengths of AB is (in cm)
View Solution
