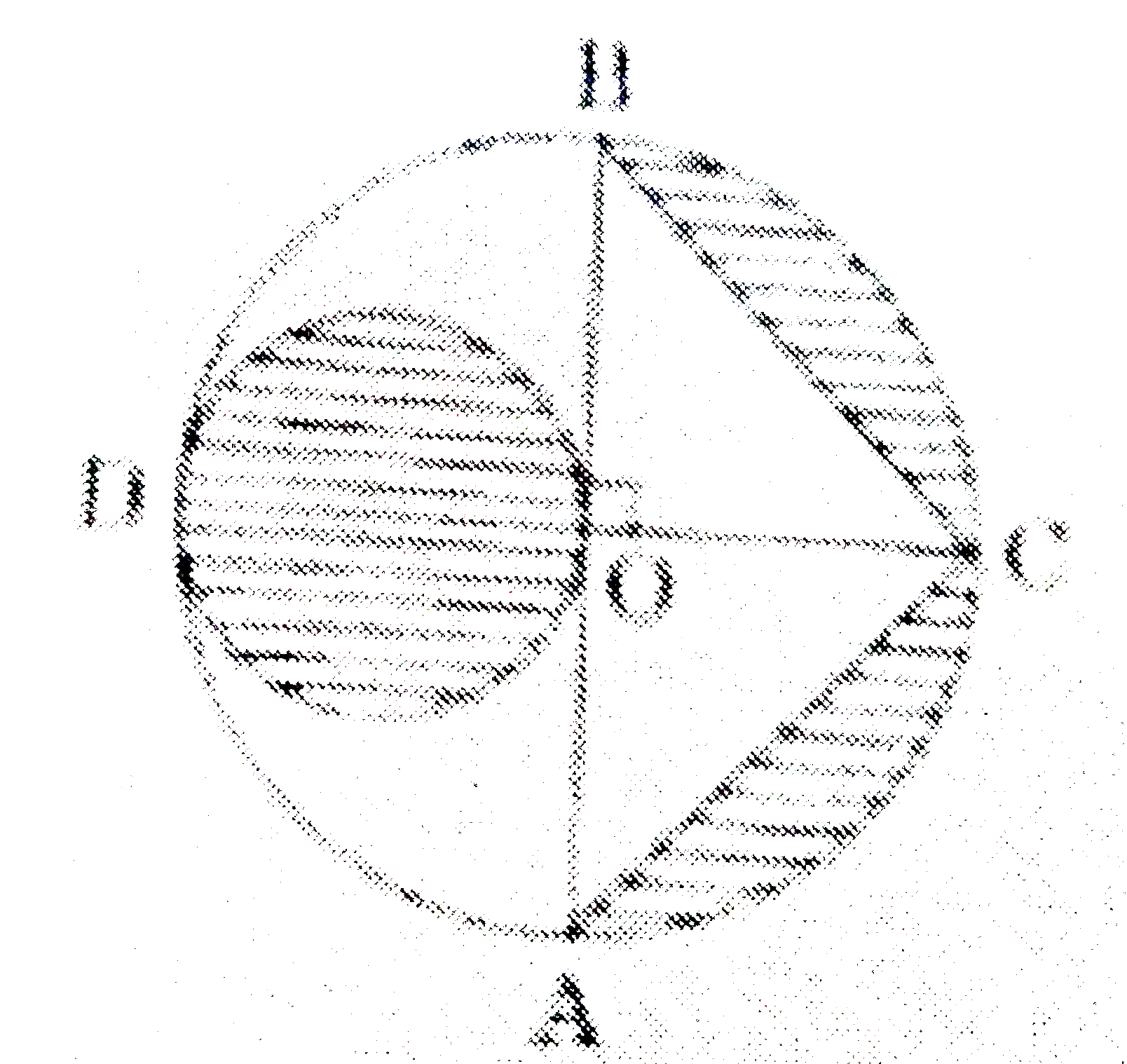
In the given figure, AB and CD are two diameters of circles ( with centre O) Perpendicular to each other and OD is the diameter of the smallest circle. If OA = 7cm, Find the area of the shaded region.
To find the area of the shaded region in the given figure, we will follow these steps:
Step 1: Identify the radius of the larger circle
Given that OA = 7 cm, we can identify that the radius of the larger circle (r1) is:
r1=OA=7cm
Hint: The radius of a circle is half of its diameter. Since OA is a radius, we can directly use its value.
Step 2: Calculate the radius of the smaller circle
Since OD is the diameter of the smaller circle, we know that the radius of the smaller circle (r2) is half of the radius of the larger circle:
r2=r12=72=3.5cm
Hint: Remember that the radius is always half of the diameter.
Step 3: Calculate the area of the larger circle
The area of a circle is given by the formula:
Area=πr2
For the larger circle:
Arealarge=πr21=227×72=227×49=154cm2
Hint: Use π≈227 for calculations involving circles.
Step 4: Calculate the area of the semicircle
Since the semicircle is half of the larger circle:
Areasemicircle=12×Arealarge=1542=77cm2
Hint: A semicircle is half of a full circle, so divide the area of the full circle by 2.
Step 5: Calculate the area of the smaller circle
Using the radius of the smaller circle:
Areasmall=πr22=227×(72)2=227×494=107828=77cm2
Hint: Ensure you square the radius correctly when calculating the area.
Step 6: Calculate the area of triangle ABC
The base AB is the diameter of the larger circle, which is:
AB=2×r1=2×7=14cm
The height OC is equal to the radius of the larger circle:
OC=7cm
Now, the area of triangle ABC is:
Area△ABC=12×base×height=12×14×7=49cm2
Hint: The area of a triangle can be calculated using the formula 12×base×height.
Step 7: Calculate the area of the shaded region
The area of the shaded region is the sum of the areas of the smaller circle and the semicircle, minus the area of triangle ABC:
Areashaded=Areasmall+Areasemicircle−Area△ABC
Areashaded=77+77−49=105cm2
Hint: Remember to add the areas of the shapes and then subtract the area of the triangle to find the shaded region.
Final Answer
The area of the shaded region is:
Areashaded=105cm2
Given that OA = 7 cm, we can identify that the radius of the larger circle (r1) is:
r1=OA=7cm
Since OD is the diameter of the smaller circle, we know that the radius of the smaller circle (r2) is half of the radius of the larger circle:
r2=r12=72=3.5cm
The area of a circle is given by the formula:
Area=πr2
For the larger circle:
Arealarge=πr21=227×72=227×49=154cm2
Since the semicircle is half of the larger circle:
Areasemicircle=12×Arealarge=1542=77cm2
Using the radius of the smaller circle:
Areasmall=πr22=227×(72)2=227×494=107828=77cm2
The base AB is the diameter of the larger circle, which is:
AB=2×r1=2×7=14cm
The height OC is equal to the radius of the larger circle:
OC=7cm
Now, the area of triangle ABC is:
Area△ABC=12×base×height=12×14×7=49cm2
The area of the shaded region is the sum of the areas of the smaller circle and the semicircle, minus the area of triangle ABC:
Areashaded=Areasmall+Areasemicircle−Area△ABC
Areashaded=77+77−49=105cm2
The area of the shaded region is:
Areashaded=105cm2
Topper's Solved these Questions
Similar Questions
If Figure - 4, AB and CD are two diameter of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. IF OA = 7 cm, then find the area of the shaded region.
 View Solution
View SolutionIn Fig. 12.27, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. IfOA=7 cm, find the area of the shaded region
View Solution
Knowledge Check
- Question 1 - Select One
In the figure, AB and CD are the diameters of the circle. What is the value of x?
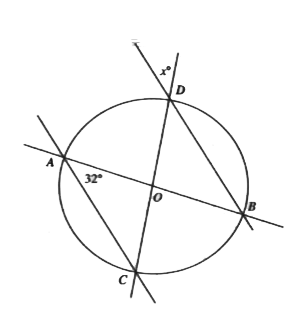 A16∘B18∘C26∘D32∘
A16∘B18∘C26∘D32∘
In Fig. 12.27, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. IfOA=7 cm, find the area of the shaded region
View SolutionIn Figure -4 AB, and CD are two diameters of a circle with centre O perpendiclualr to each other and OD is the diameter of the circle . If OA = 7 cm , then find the carea of the shaded region .
 View Solution
View SolutionIn Figure, AB and CD are two diameters of a circle perpendicular to each other and OD is the diameter of the smaller circle. If OA=7 cm , find the area of the shaded region.
View SolutionIn the figure, AB is a diameter of the circle with centre O and OA = 7cm. Find the area of the shaded region
View SolutionIn the given figure, AB and XY are diameters of a circle with centre O. If ∠APX=30∘, find:
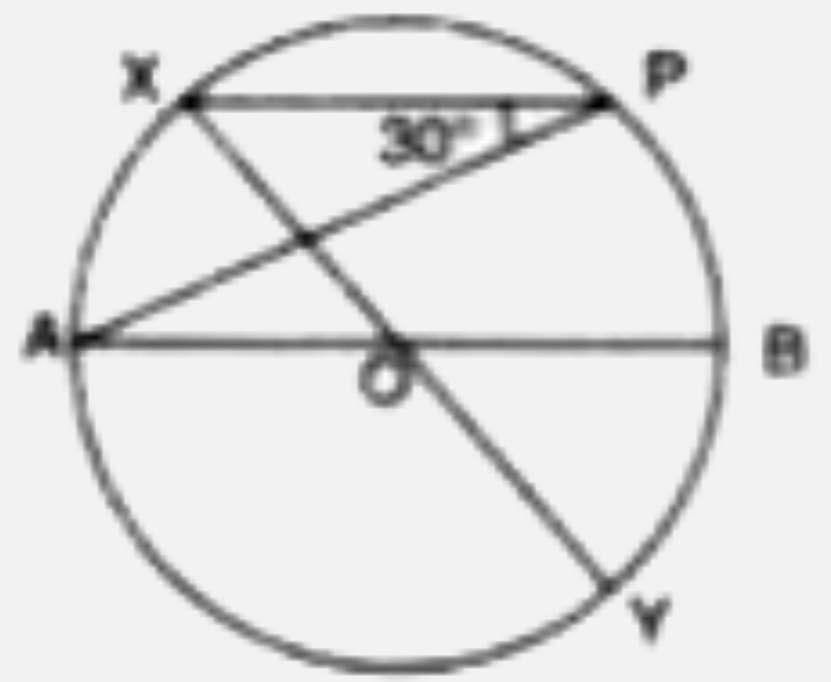
∠AOXView SolutionIn the given figure, AB and XY are diameters of a circle with centre O. If ∠APX=30∘, find:

∠APYView SolutionIn the given figure, AB and XY are diameters of a circle with centre O. If ∠APX=30∘, find:
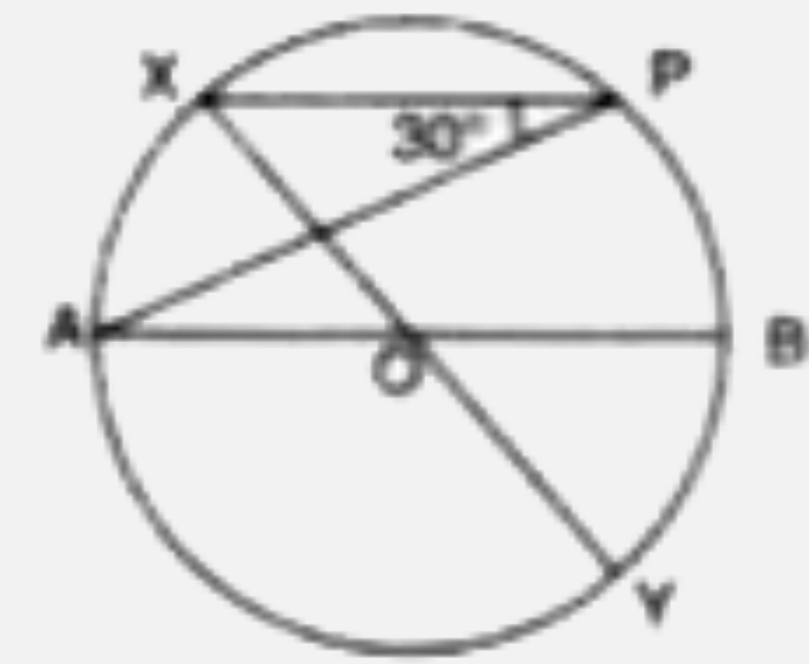
∠BPYView Solution

