In the given figure, ABCD is a cyclic quadrilateral in which DC is produced to E and CF is drawn parallel to AB such that ∠ADC=95∘ and ∠ECF=20∘. The, ∠BAD=?
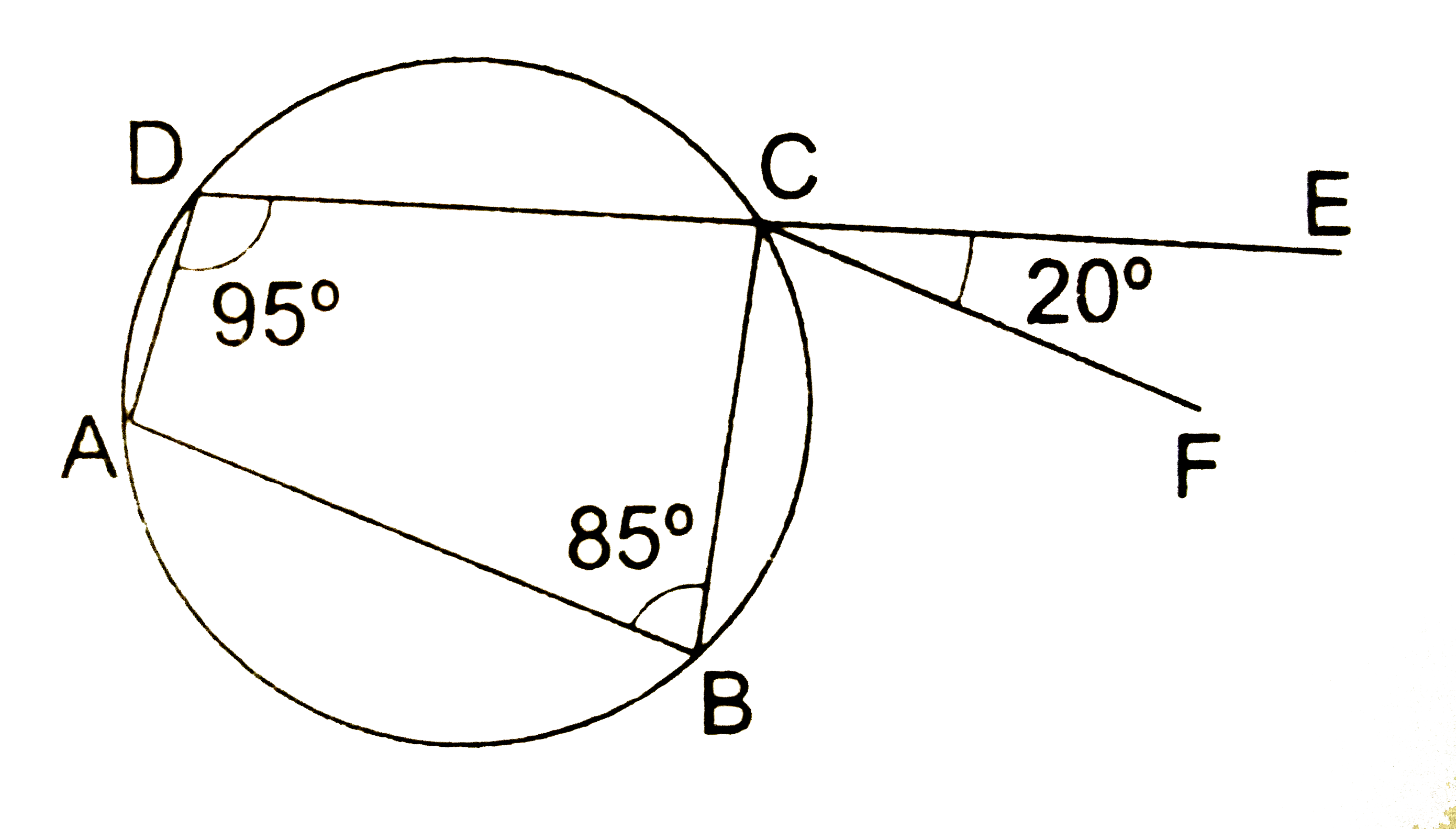
95∘
85∘
105∘
75∘
The correct Answer is:C
∠ABC+∠ADC=180∘⇒∠ABC+95∘=180∘⇒∠ABC=85∘
Now, VF∣∣AB and CB is the transversal
∴∠BCF=∠ABC=85∘ [alt. int. ∠s]
⇒∠BCE=85∘+20∘=105∘
⇒∠DCB=180∘−105∘=75∘
Now, /_BAD+∠BCD=180∘⇒∠BAD+75∘=180∘⇒∠BAD=105∘
Topper's Solved these Questions
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Multiple Choice Questions (Mcq)
5 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
Similar Questions
Knowledge Check
In a given figure, ABCD is cyclic quadrilateral, in which ∠DAB=80∘, then measures of ∠DCE is
 A80∘B90∘C120∘D140∘
A80∘B90∘C120∘D140∘In the given figure, ABCD is a cyclic quadrilateral and AB is diameter. ∠ADC=140∘, then find ∠BAC :
 A45∘B40∘C50∘Dnone of the above
A45∘B40∘C50∘Dnone of the above
In the given figure ABCD is a cyclic quadrilateral in which AE is drawn parallel to CD and BA is produced. If ∠ABC=92∘ and ∠FAE=20∘, Find ∠BCD.

View SolutionABCD is cyclic quadrilateral in which AB and CD when produced meet in E and EA = ED. Prove that (i) AD || BC (ii) EB=EC
View SolutionIn Figure, ABCD is quadrilateral inscribed in a circle with centre O.CD is produced to E such that ∠ADE=950and ∠OBA=300. Find ∠OAC
View SolutionIn the given figure, ABCD is cyclic quadrilateral. If ∠BCD=110∘and∠ABD=60∘ measures of ∠DAEand∠ADB.
View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral.If side BC is produced upto point E and ∠DAB=95∘, then find the value of ∠DCE.

View SolutionIn the given figure ABCD is, ABCD is a quadrilateral in which AB∣∣DC and AD∣∣BC prove that ANGLEADC=ANGLEABC.

View Solution
