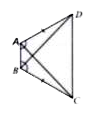
In the given figure, ABCD is a quadrilateral in which AD = BC and ∠DAB=∠CBA.
Prove that (i) ΔABD≅ΔBAC,
(ii) BD = AC,
(iii) ∠ABD=∠BAC.

Video Solution
Text Solution
GIVEN A quadrilateral ABCD in which AD = BC and ∠DAB=∠CBA.
TO PROVE (i) ΔABD≅ΔBAC, (ii)BD=AC, (iii)∠ABD=∠BAC.
PROOF (i) In ΔABDandΔBAC, we have
AD=BC (given)
∠DAB=∠CBA (given)
AB=BA (common)
∴ ΔABD≅ΔBAC (SAS-criteria).
(ii) As shown above, ΔABD≅ΔBAC.
∴ BD=AC (c.p.c.t.).
(iii) And, ∠ABD=∠BAC (c.p.c.t.).
|
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9A
27 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9B
16 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)
37 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)
22 Videos
Similar Questions
Knowledge Check
In the given figure AD=BC,AC=BD. Then ΔPAB is
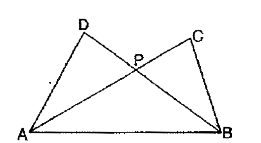 AequilateralBright angledCscaleneDisosceles
AequilateralBright angledCscaleneDisosceles
ABCD is quadrilateral in which AD=BCand∠DAB=∠CBA (see figure). Prove that

BD=AC
View SolutionABCD is quadrilateral in which AD=BCand∠DAB=∠CBA (see figure). Prove that
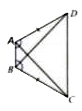
∠ADB=∠BCA.
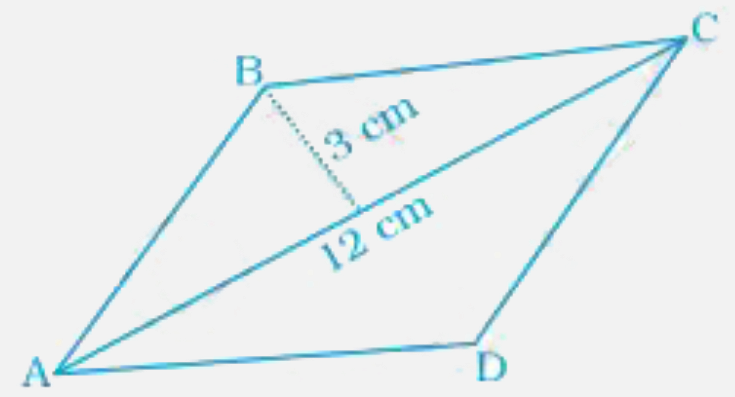
View SolutionThe figure ABCD is a quadrilateral in which AB = CD and BC = AD. Its area is
View SolutionIn the given figure ABCD is, ABCD is a quadrilateral in which AB∣∣DC and AD∣∣BC prove that ANGLEADC=ANGLEABC.

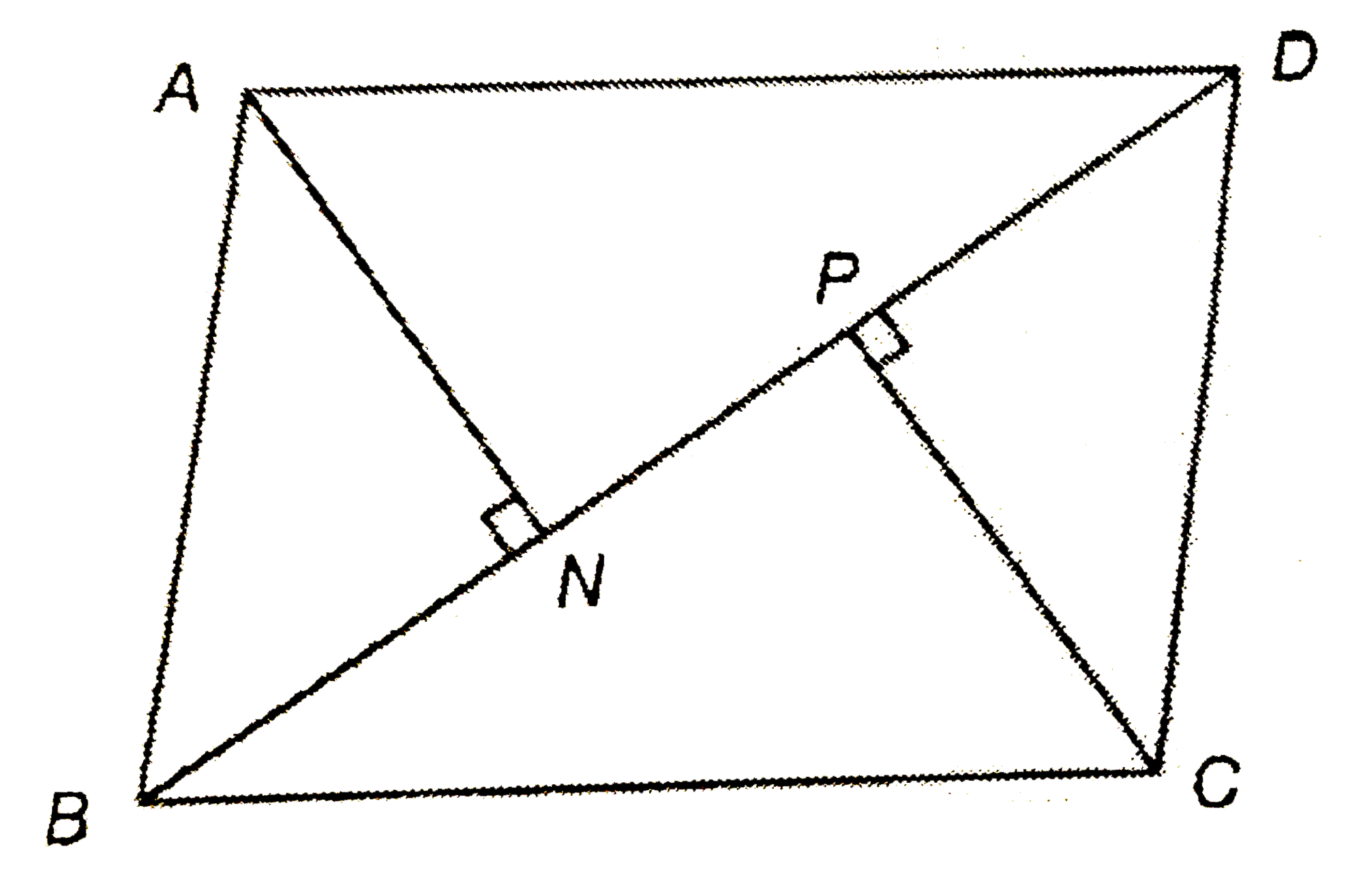
View SolutionIn the given figure, ABCD is a parallelogram in which AN and CP are perpendiculars on diagonal BD. Prove that :
(i) ΔADN=ΔCBP
(ii)AN=CP
View SolutionIf ABCD is a quadrilateral in which ABCD and AD=BC, prove that ∠A =∠B.
View Solution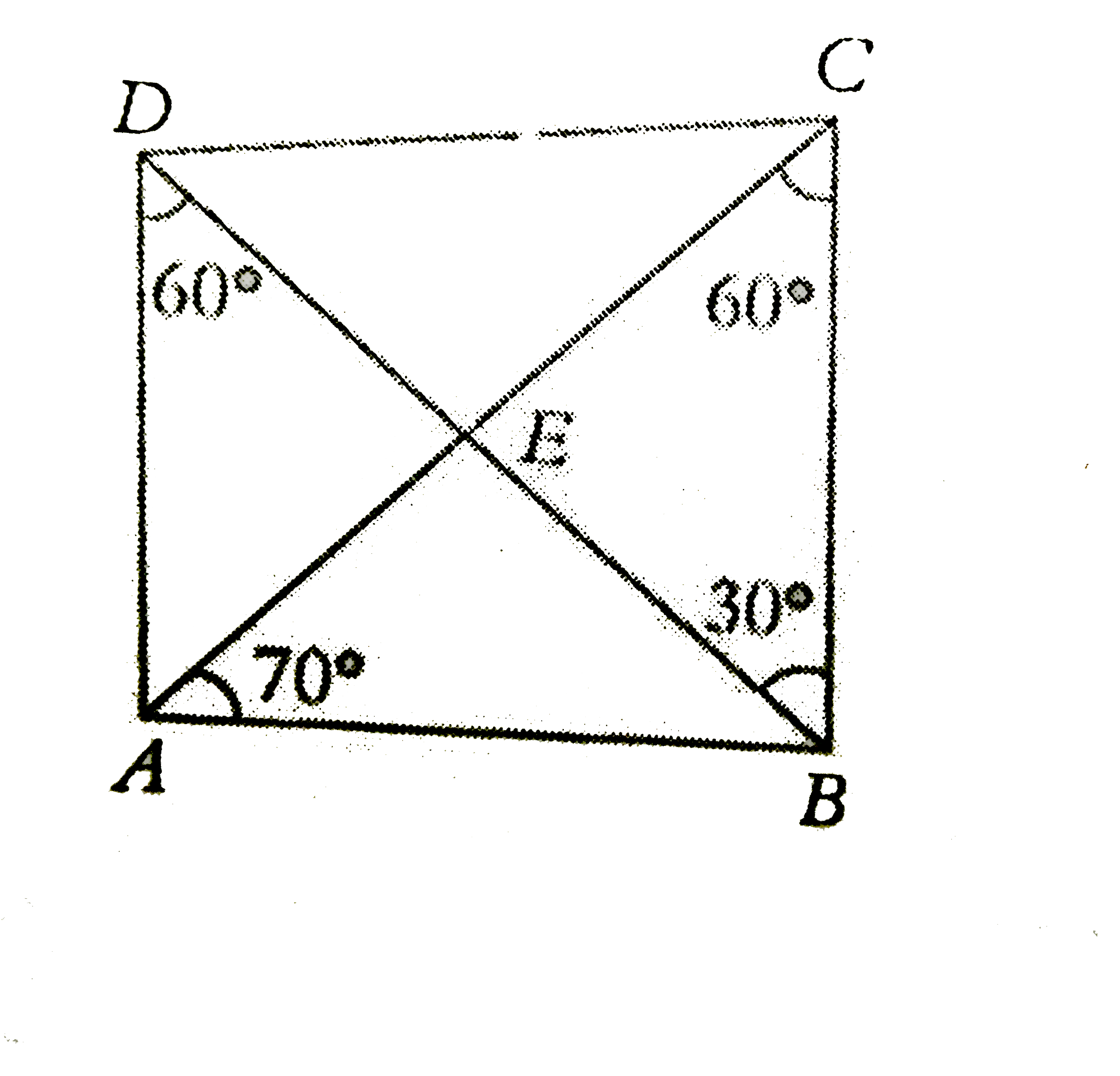
In the given figure, ABCD is a quadrilateral ∠ADB=60∘,∠BAC=70∘,∠DBC=30∘, and
View Solution