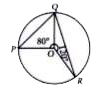
In the given figure, O is the centre of a circle in which ∠AOC=100∘. Side AB of quad. OABC has been produced to D. Then, ∠CBD=?
A
50∘
B
40∘
C
25∘
D
80∘
Video Solution
Text Solution
The correct Answer is:A
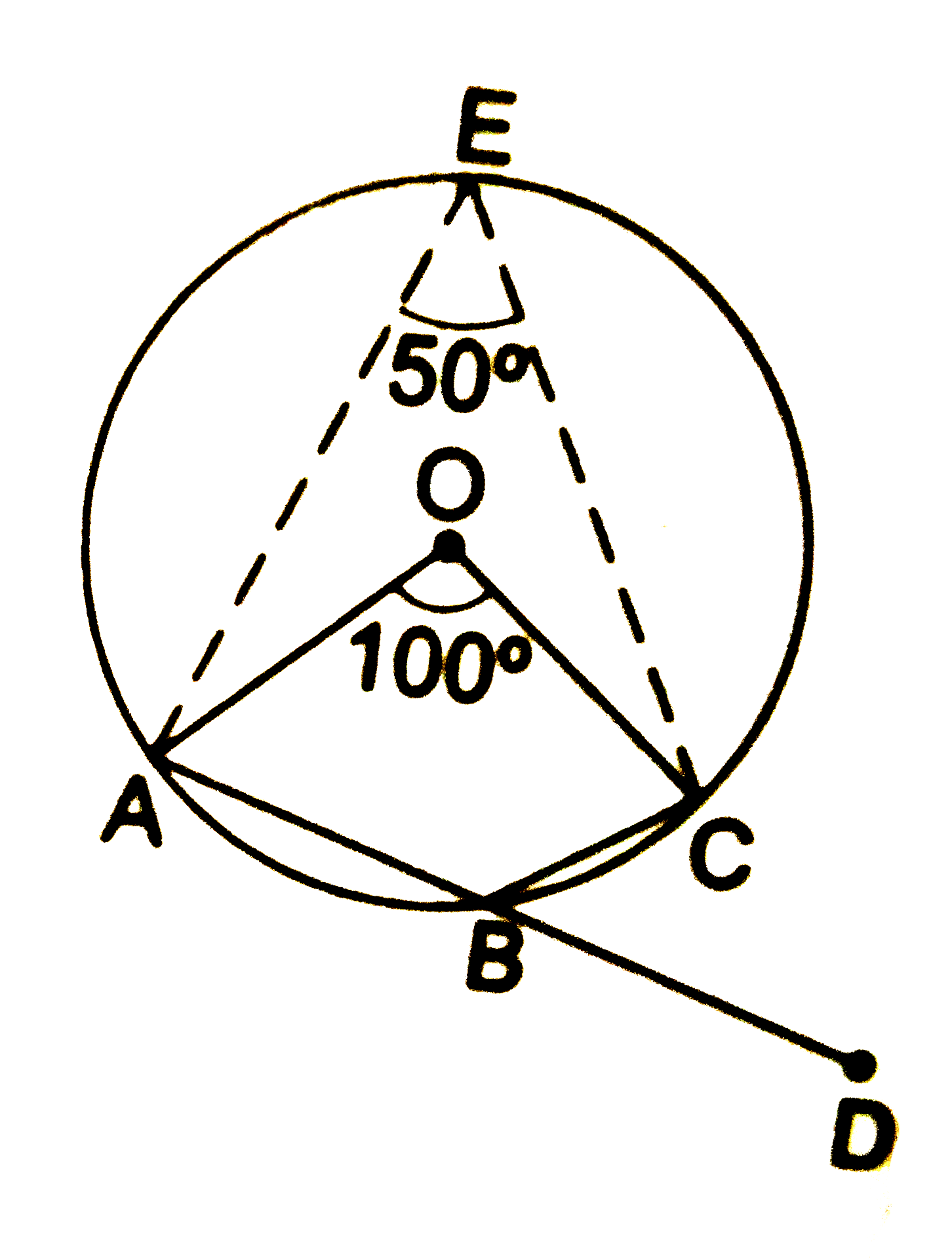
Take a point E on the remaining part of circumference of the circle.
Join AE and CE.
∠AEC=12∠AOC=12×100∘=50∘
Now, side AB of cyclic quad. ABCE has been produced to D.
So, ext. ∠CBD=∠AEC=50∘
|
Topper's Solved these Questions
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Multiple Choice Questions (Mcq)
5 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
Similar Questions
Knowledge Check
In the given figure, O is the centre of circle, ∠AOB=100∘. Find ∠BCD :
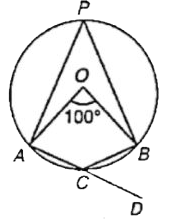 A80∘B60∘C50∘D40∘
A80∘B60∘C50∘D40∘In the given figure, O is the centre of the circle. The value of x is
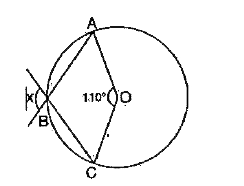 A75∘B55∘C125∘D110∘
A75∘B55∘C125∘D110∘In the given figures, value of y (O is the centre of the circle) is
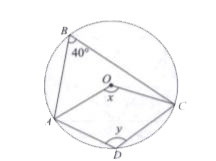 A100∘B120∘C130∘D140∘
A100∘B120∘C130∘D140∘
In the given figure, O is the centre of a circle, ∠AOB=40∘ and ∠BDC=100∘, find ∠OBC.
View SolutionIn Figure, it is given that O is the centre of the circle and ∠AOC=1500. Find ∠ABC
View SolutionIn the figure, O is the centre of the circle such that ∠AOC−140∘, then ∠ABC=…….

View SolutionIn the figure, O is the centre of the circle. Prove ∠AOC=∠AFC+∠AEC.
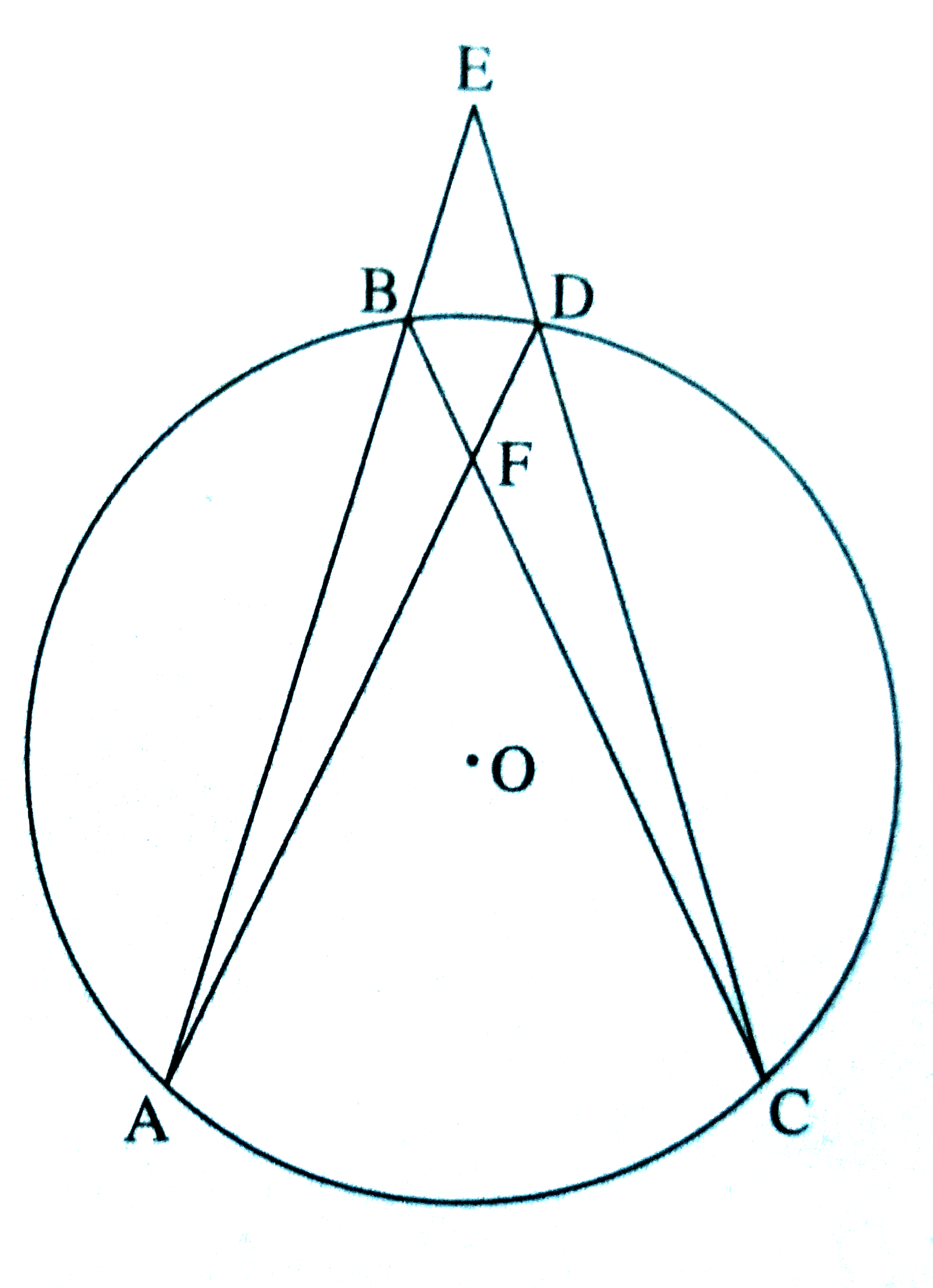
View SolutionIn the given figure, O is the centre of the circle and ∠AOC=100∘. Find the ratio of ∠ADC:∠ABC :
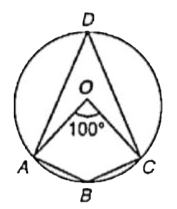
View Solution