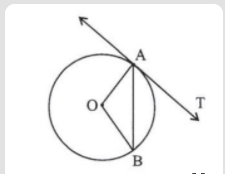
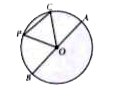
In the given figure, O is the centre of a circle, PQ is a chord and PT is the tangent at P. If ∠POQ=70∘, then ∠TPQ is equal to

35∘
45∘
55∘
70∘
Mark a point R in the alternate segment.
Join PR and QR.
Then, ∠PRQ=12∠POQ=12×70∘=35∘.
Now, ∠TPQ=∠PRQ=35∘[angles in alternate segments].
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Assertion-and-Reason1videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Test Yourself20videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Multiple Choice Questions (Mcq)15videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Multiple Choice Questions (Mcq)30videos
ARITHMETIC PROGRESSION
- BOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - Test Yourself10videos
CONSTRUCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure, O is the centre of a circle , AB is a chord and AT is the tangent at A. If ∠AOB=100∘ then ∠BAT is equal to
A40∘B50∘C90∘D100∘ - Question 2 - Select One
In figure, if O is the centre of a circle, PQ is a chord and the tangent PR at P makes an angle of 50∘ with PQ, then ∠POQ is equal to
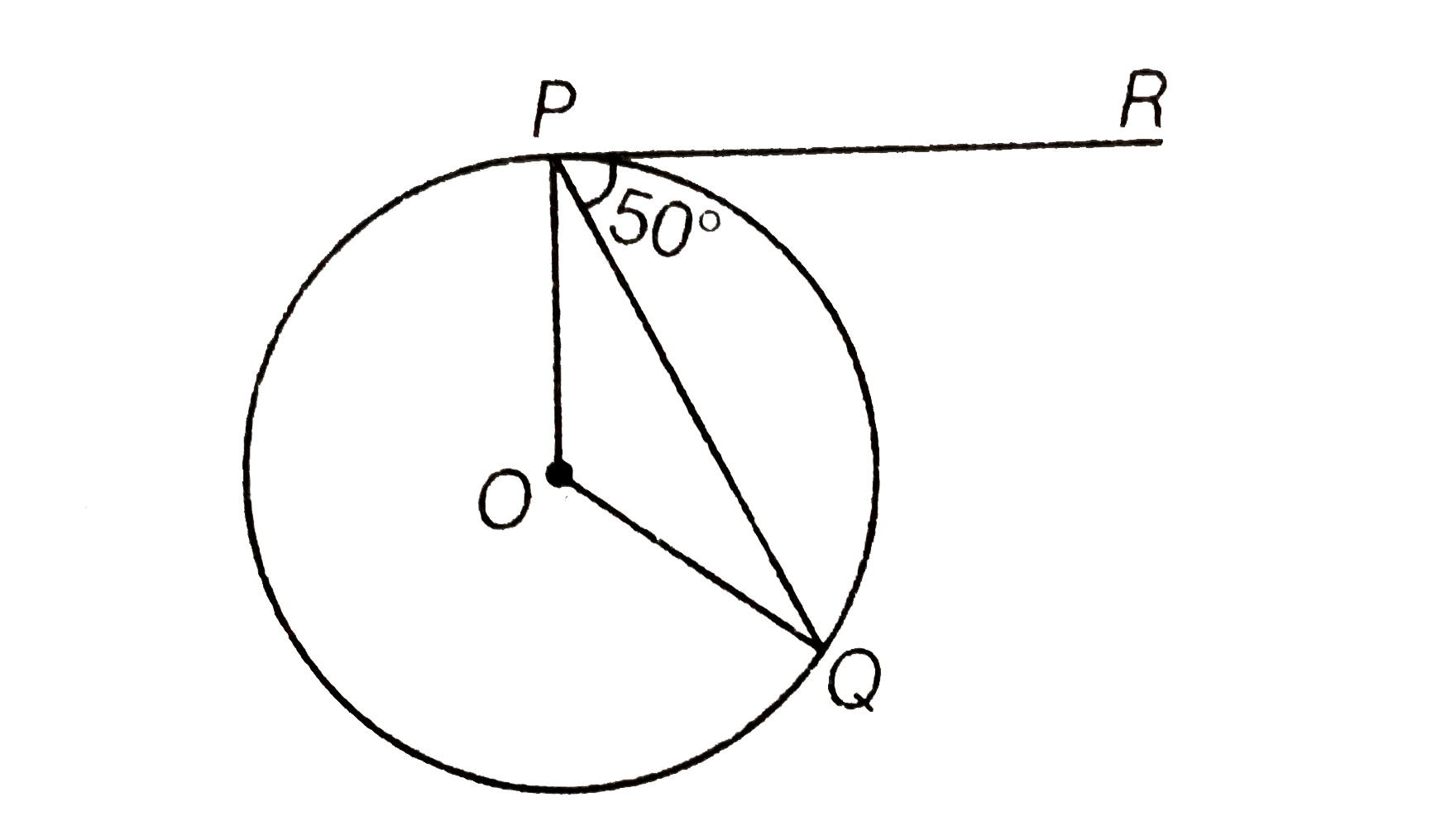 A100∘B80∘C90∘D75∘
A100∘B80∘C90∘D75∘
In the given figure, O is the centre of the circle.

Name all chords of the circle.View SolutionPQ is a chord of a circle with centre O and PT is the tangent at P such that ∠QPT=70∘. Then the measure of ∠PRQ is equal to :
(A) 135∘ (B) 150∘ (C) 120∘ (D) 110∘View SolutionIn Fig , O is the centre of a circle , PQ is a chord and the tangent PR at P makes an angle of 50∘ with PQ. Find ∠POQ .
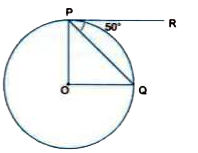 View Solution
View SolutionIn the given figure, O is the centre of the circle.

Name a chord, which is not the diameter of the circle.View SolutionIn the given figure, PQ is a chord of a circle with centre O and PT is a tangent. If ∠QPT=60∘ find ∠PRQ
View SolutionIn given figure, O is the centre of the circle.
A chord, which is not the diameter of the circle isView Solution