In the given figure, two circles touch each other at and is a tangent to both the circles. The mesure of is
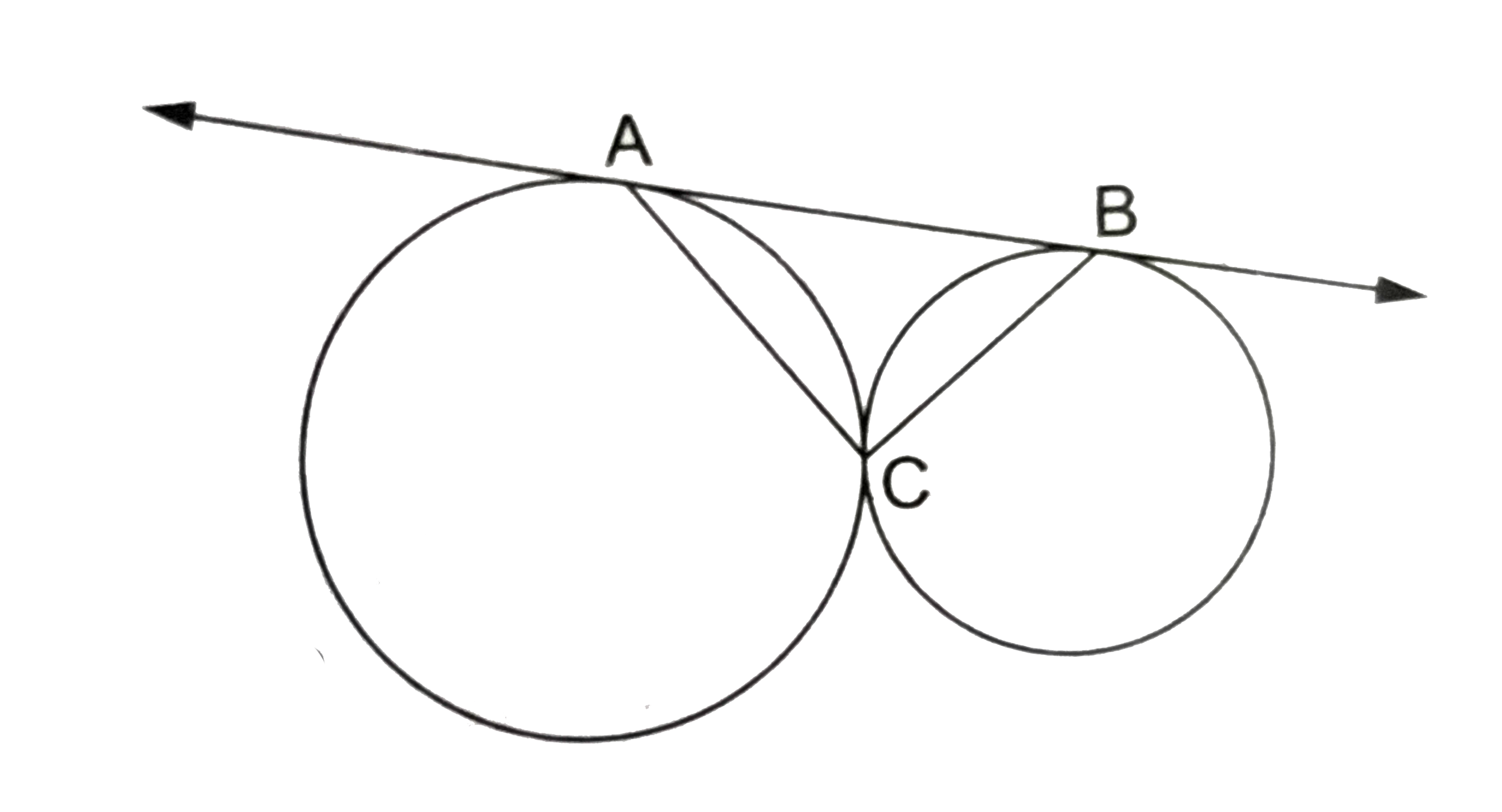
Draw a tangent to the circles at point . Let it meet at .
Then, and

Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Assertion-and-Reason1videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Test Yourself20videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Multiple Choice Questions (Mcq)15videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Multiple Choice Questions (Mcq)30videos
ARITHMETIC PROGRESSION
- BOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - Test Yourself10videos
CONSTRUCTIONS
Similar Questions
In the given figure two circles touch each other at the point C. Prove that the common tangent at P and Q.
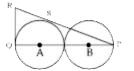
View SolutionIn the given figure. Two identical circles of radius 4 cm touch each other. A and B are the centres of the two circles. If RQ is a tangent to the circle, then what is the length (in cm) of RQ?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The two circles touch each other if
Ac=√a2+b2B1c=1a2+1b2Cc=1a2+1b2Dc=1a2+b2 - Question 2 - Select One
In the given figure. Two identical circles of radius 4 cm touch each other. A and B are the centres of the two circles. If RQ is a tangent to the circle, then what is the length (in cm) of RQ?
 A3√3B2√6C4√2D6√2
A3√3B2√6C4√2D6√2
Two equal circles touch each other externally at C and AB is a common tangent to the circles. Then, ∠ACB= 60o (b) 45o (c) 30o (d) 90o
View SolutionIn the figure, two circles intersect each other in points P and Q. If tangent from point R touch the circles at S and T, then prove that RS=RT.
 View Solution
View SolutionIn the given figure, there are two circles with centers A and B. The common tangent to the circles touches them, respectively,at P and Q. AR is 40cm and AB is divided by the point of contact of the circles in the ratio 5:3
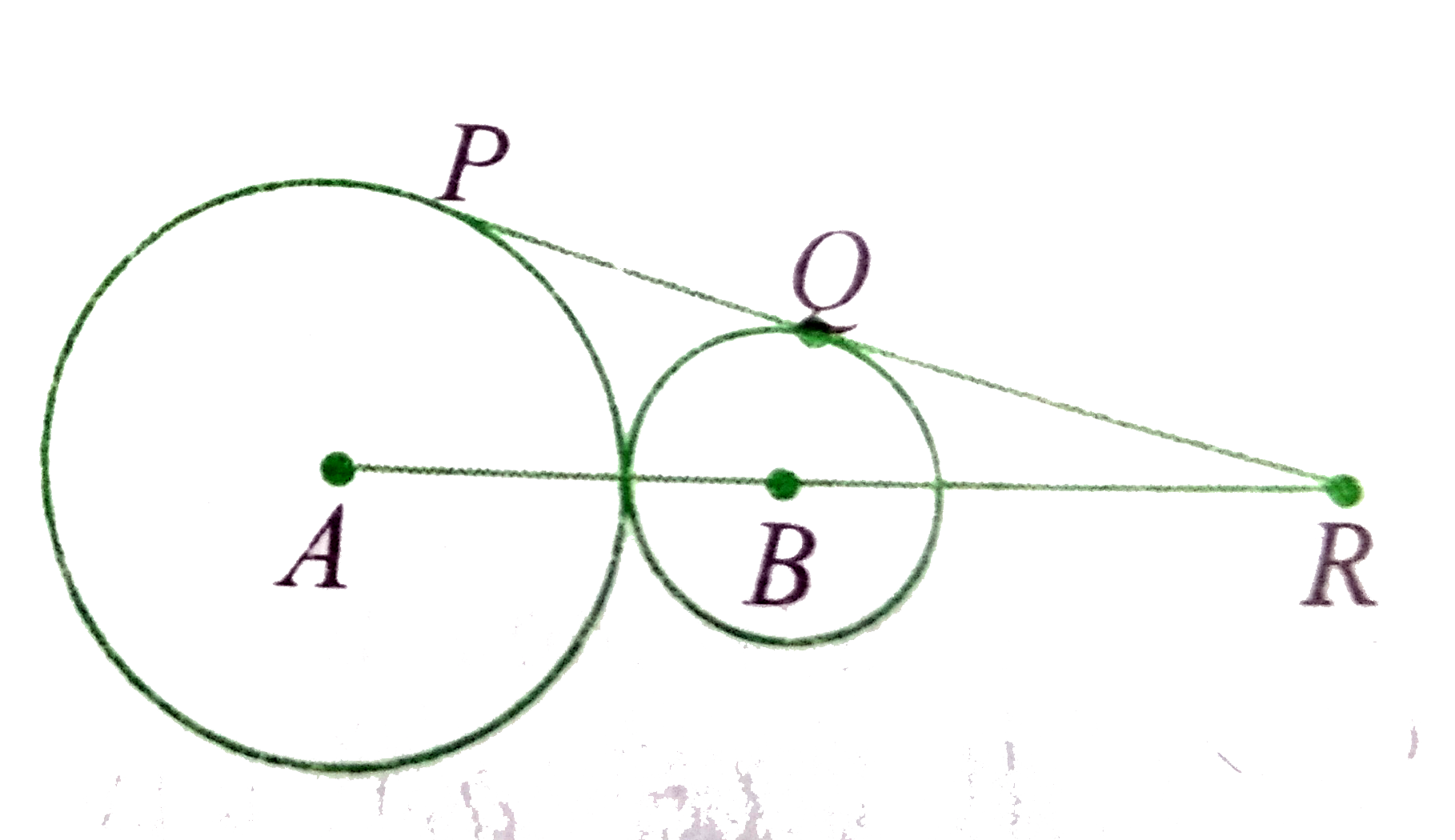
The length of QR isView SolutionIn the given figure two small circles touch each other externally at the centre of a big circle and these small circles are touched internally by a big circle of radius 74cm. Find the area of the shaded region
 View Solution
View SolutionIn the adjoining figure ∠ACE is a right angle there are three circles which just touch each other and AC and EC are the tangents to all the three circles. What is the ratio of radii of the largest circle to that of the smallest circle?
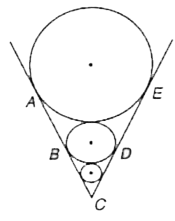 View Solution
View SolutionIn figure, two circles intersect each other at points S and R. Their common tangent PQ touches the circle at points P,Q. Prove that, ∠PRQ+∠PSQ=180∘.
 View Solution
View Solution

