In the given the length of arcs AB and BC are in the ratio 3:2.
If ∠AOB=96∘ find
∠BOC
The correct Answer is:64∘
To solve the problem, we need to find the angle BOC given the lengths of arcs AB and BC are in the ratio 3:2 and angle AOB is 96 degrees.
1. Understand the Given Information:
- The lengths of arcs AB and BC are in the ratio 3:2.
- Angle AOB = 96 degrees.
2. Use the Property of Circles:
- The angles subtended by arcs at the center of the circle are in the same ratio as the lengths of the arcs. Therefore, if the ratio of the lengths of arcs AB and BC is 3:2, the ratio of the angles AOB and BOC will also be 3:2.
3. Set Up the Ratio:
- Let angle BOC be represented as x.
- According to the ratio, we can write:
Angle AOBAngle BOC=32
- Substituting the known value:
96x=32
4. Cross Multiply to Solve for x:
- Cross multiplying gives:
3x=2×96
- Simplifying the right side:
3x=192
5. Divide to Find x:
- Now, divide both sides by 3:
x=1923=64
6. Conclusion:
- Therefore, angle BOC = 64 degrees.
Final Answer:
Angle BOC = 64 degrees.
- The lengths of arcs AB and BC are in the ratio 3:2.
- Angle AOB = 96 degrees.
- The angles subtended by arcs at the center of the circle are in the same ratio as the lengths of the arcs. Therefore, if the ratio of the lengths of arcs AB and BC is 3:2, the ratio of the angles AOB and BOC will also be 3:2.
- Let angle BOC be represented as x.
- According to the ratio, we can write:
Angle AOBAngle BOC=32
- Substituting the known value:
96x=32
- Cross multiplying gives:
3x=2×96
- Simplifying the right side:
3x=192
- Now, divide both sides by 3:
x=1923=64
- Therefore, angle BOC = 64 degrees.
Angle BOC = 64 degrees.
Topper's Solved these Questions
Similar Questions
In the given the length of arcs AB and BC are in the ratio 3:2.
If ∠AOB=96∘ find
∠ABC
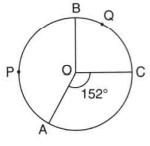
View SolutionIn the given figure, lengths of arcs APB and BQC are in the ratio 5:3 and angle AOC=152∘, find angle ACB and angle BAC.
View SolutionIn the given figure , the lengths of arc AB and are BC arc in the ratio 3: 2 if ∠AOB=96∘, find
(i)∠CAB(ii)∠ADB

View SolutionIn circle given below . O is its centre and lengths of chords AB and CD are in the ratio 5 :3
If angle AOB = 100∘, find :
(i)∠COD

View SolutionIn the given figure, O is the centre of the circle and the length of arc AB is twice the length of arc BC.
if ∠AOB=100∘ find ∠BOC
View SolutionIn the given 'O' is the centre of the circle, Arc AB=ArcBC=Cd.If∠OAB=48∘, find:
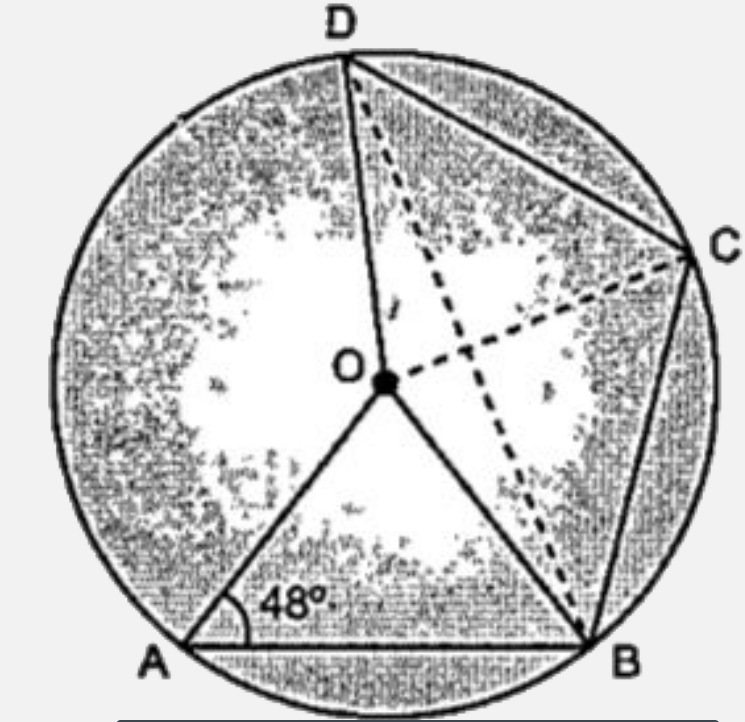
∠OBD
View SolutionIn the given arc AB= twice are BC and ∠AOB=80∘ find:
∠BOC
View SolutionIn the given arc AB= twice are BC and ∠AOB=80∘ find:
∠OAC
View SolutionIn the given circle. Arc APB and are BQC are in the ratio 2: 5 and O is centre of the circle.

If angle AOB = 44∘ : Find angle AOC.
View SolutionTwo supplementary angles are in the ratio 2:3. Find the angles.
View Solution
