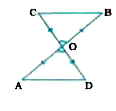
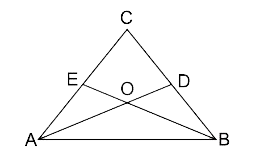
In the givne figure, OA = OB and OP = OQ.
Prove that (i) PX = QX, (ii) AX = BX.
ΔOQA≅ΔOPB as OQ=OP,OA=OB,∠AOQ=∠BOP.
∴ ∠A=∠B.
ΔAXP≅ΔBXQ as ∠A=∠B.
ΔAXP≅ΔBXQ as ∠A=∠B,∠AXP=∠BXQ,(OA−OP)=(OB−OQ).
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)
37 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)
22 Videos
Similar Questions
Knowledge Check
In figure, OP bisects ∠BOCandOQ bisects ∠AOC, then ∠POQ is
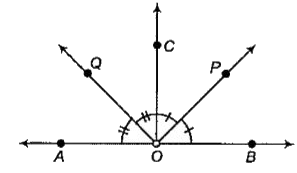 A90∘B75∘C105∘D80∘
A90∘B75∘C105∘D80∘
In the following figure, OA = OC and AB = BC. Prove that :
(i) ∠APB=90∘
(ii) ΔAOD≅ΔCOD
(iii) AD=CD
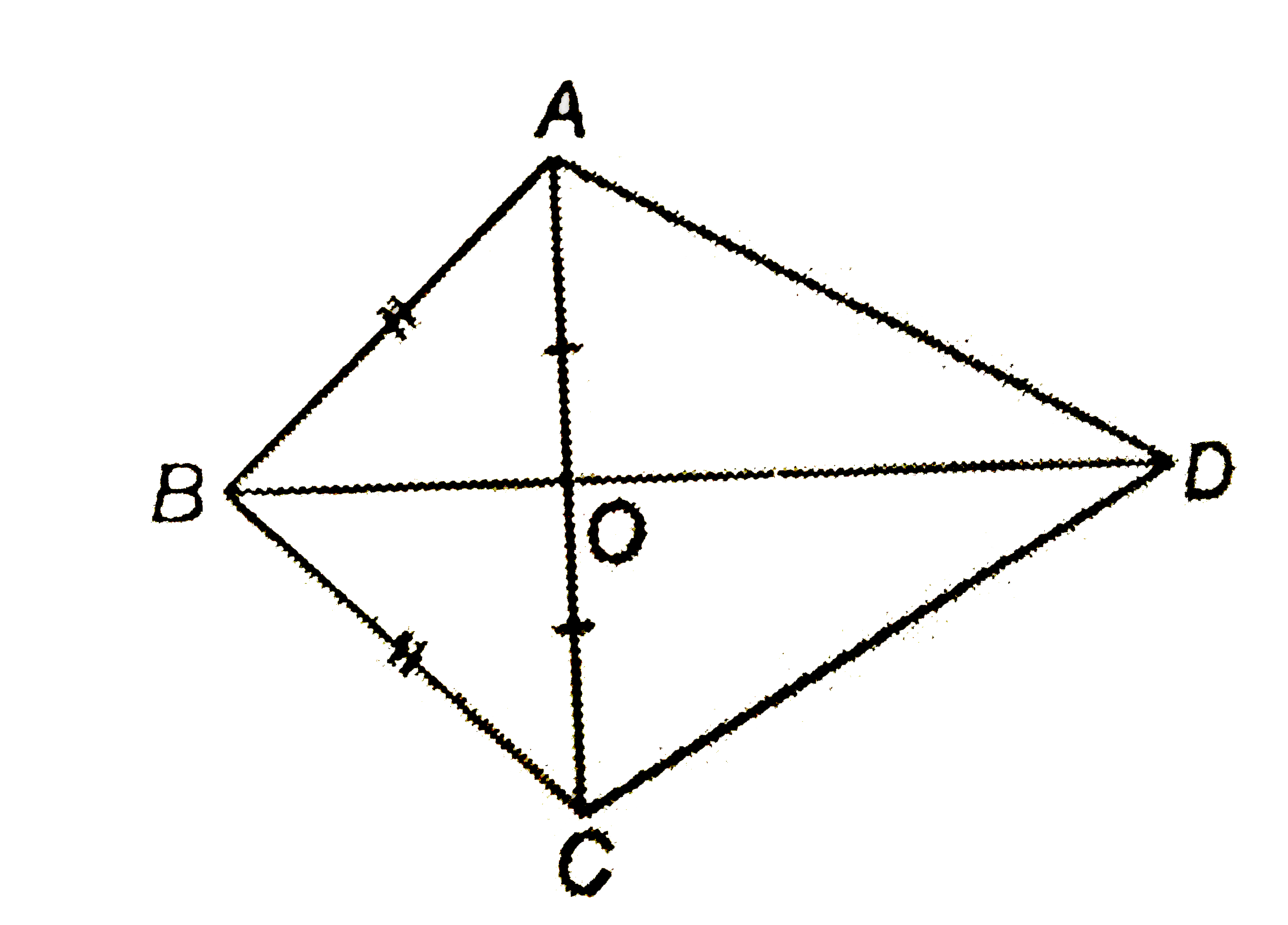
View SolutionIn the given figure, Oa = OB and OC = OD. Which is the criteria to prove
ΔAOC≅ΔBOD.

View SolutionIn the given figure DA⊥OP and DB⊥OQand ∠ADB=170∘ find ∠AOB.
View SolutionIn the adjoining figure, QX and RX are the bisectors of the angles Q and R respectively of the angles Q and R respectively of the triangle PQR. If XS⊥PQ. Prove that :
(i) ΔXTQ≅ΔXSQ
(ii) PX bisects angle P.

View SolutionIn figure OA∗OB=OC∗OD. Show that ∠A=∠Cand ∠B=∠D.
View SolutionIn the given figure A, B and C are points on OP, OQ and OR respectively such that AB||PQ and BC||QR. Show that AC||PR.

View SolutionIn the given figure ∠ABC=∠BAC , D and E are pointts on BC and AC respectively such that DB = AE . If AD and BE intersect at O then prove that OA = OB
View Solution