In trapezium PQRS, side PQ∣∣ side SR, AR=5AP, AS=5AQ then prove that SR=5PQ by completing the following activity.
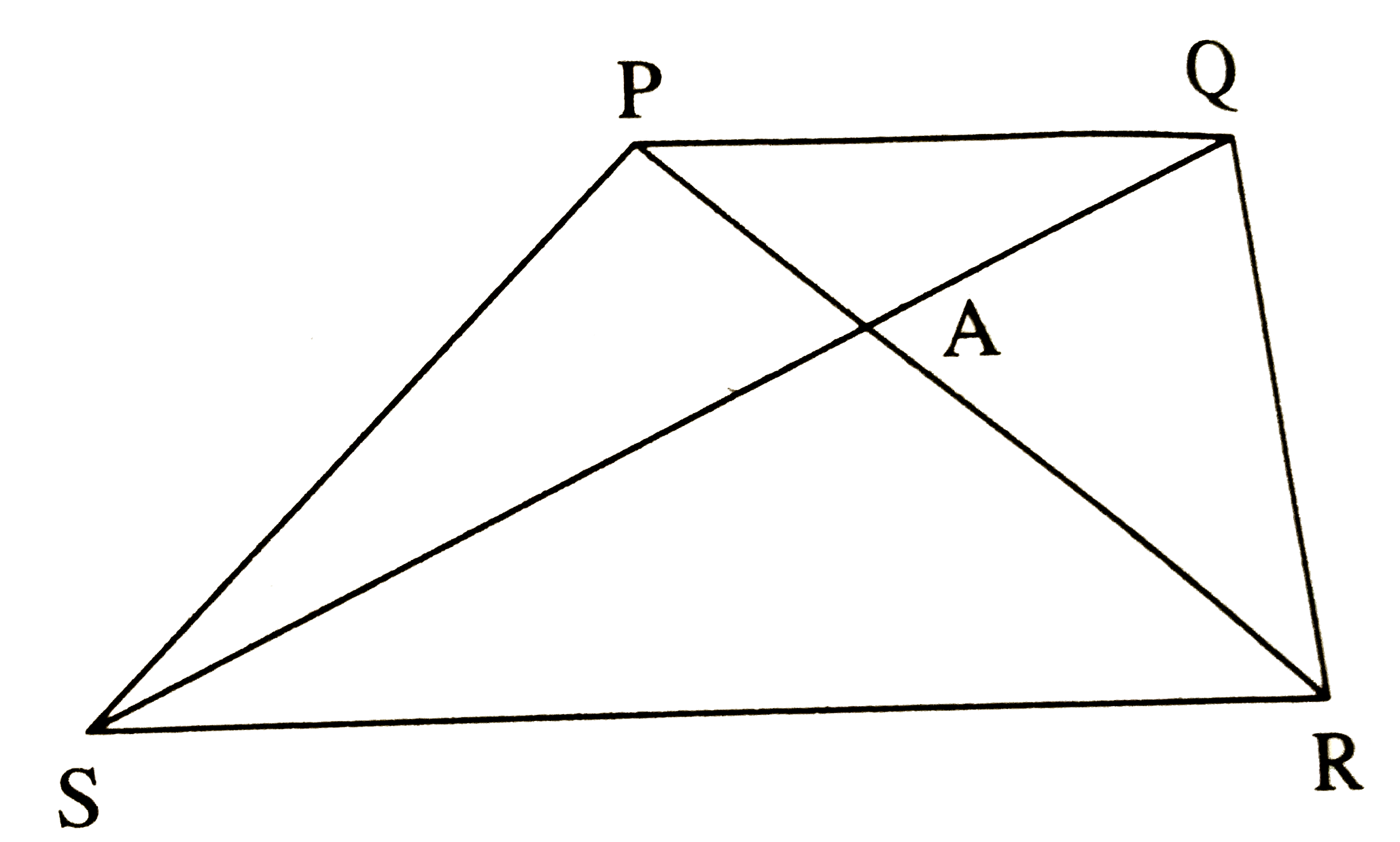
In ΔPQA and ΔRSA,
∠PQA≅∠RSA……(□)
∠PAQ≅∠RAS....(□)
∴ΔPQA~ΔRSA ......(□)
PQSR=□AR.........(Corresponding sides of similar triangles).....(1)
Substituting AR=5AP in (1)
∴PQSR=□5AP
∴PQSR=□5
∴SR=5PQ
In ΔPQA and ΔRSA,
∠PQA≅∠RSA……(Alternate angle)
∠PAQ≅∠RAS....(Vertically opposite angles)
∴ΔPQA~ΔRSA ......("AA" test of similarity)
PQSR=APAR.........(Corresponding sides of similar triangles).....(1)
Substituting AR=5AP in (1)
∴PQSR=AP5AP
∴PQSR=15
∴SR=5PQ
Topper's Solved these Questions
- SIMILARITYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - 2.5 (4 mark each)
3 Videos
- SIMILARITYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - EXAMPLE TYPE
50 Videos
- SIMILARITYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - 2.3 (2 mark each)
10 Videos
- QUADRATIC EQUATIONS BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUADRATIC EQUATIONS EXERCISE - ASSIGNEMENT 2.4
8 Videos
- STATISTICSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - STATISTICSEXERCISE - EXAMPLES FOR PRACTICE (MCQs)
35 Videos
Similar Questions
Given: In trapezium PQRS, sides PQ∣∣ sides SR,AR=5AP,AS=5AQ, then prove that SR=5PQ.
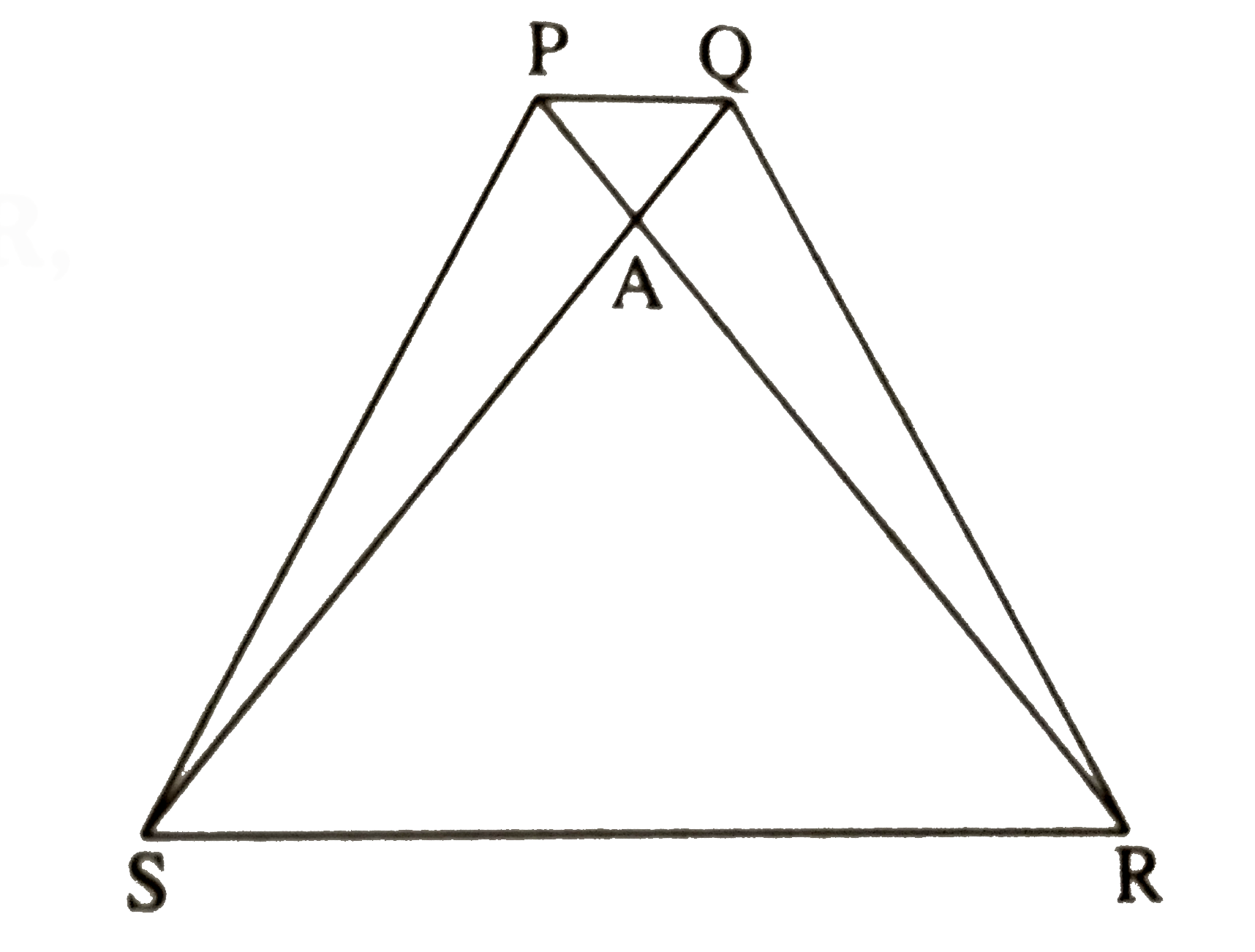
View SolutionGiven : In trapezium PQRS,sPQ∣∣sSR,AR=5AP,AS=5AQthen prove that,SR=5PQ
View SolutionGiven : In trapezium PQRS, side PQ||SR, AR = 5 AP, AS = 5 AQ, then prove that SR=5 PQ.
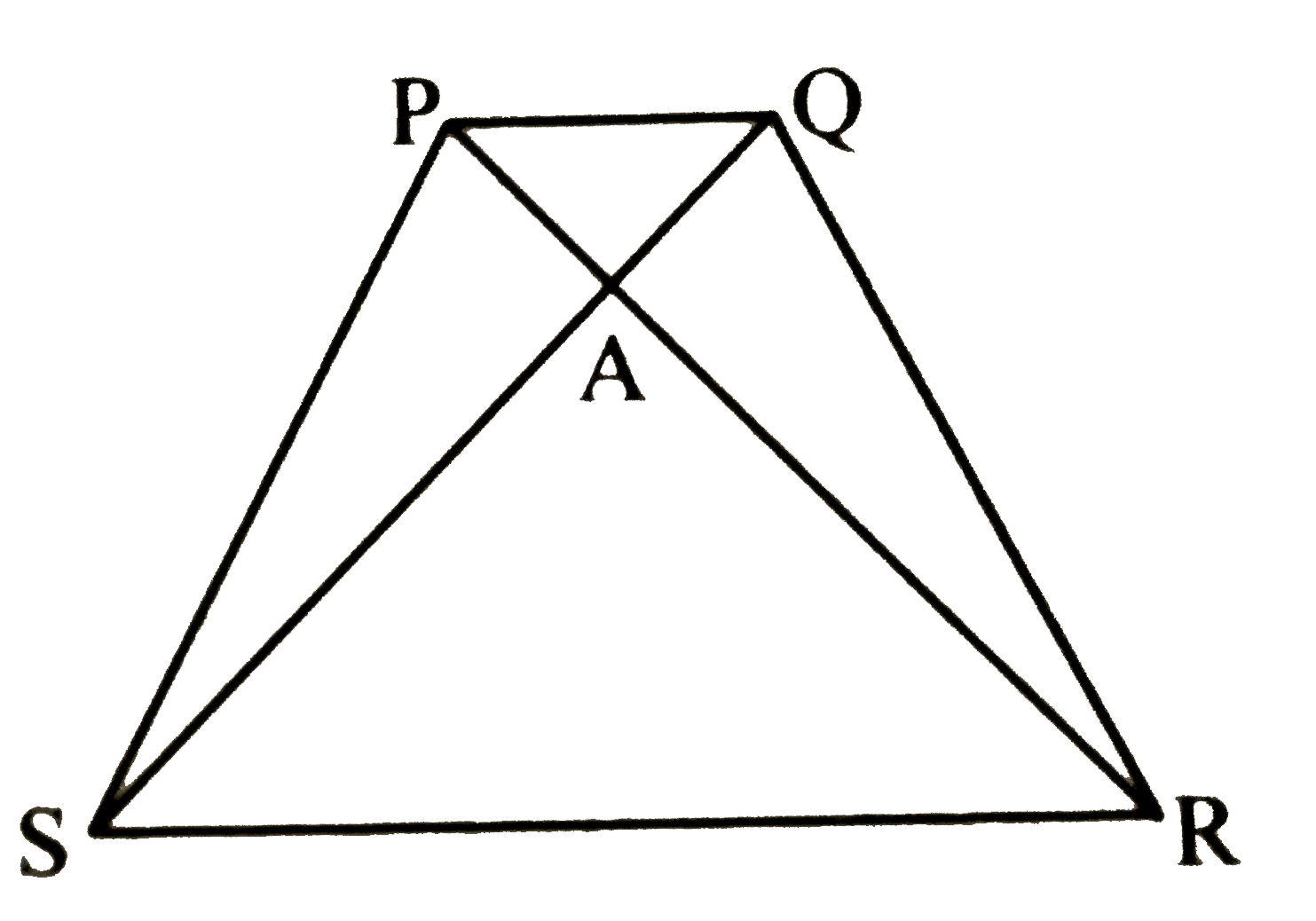
View SolutionIn trapezium PQRS,side PQ∣∣ sideSR. Diagonals PR and QS intersect each other at point M. PQ=2RS. Prove that PM=2RM and QM=2SM.
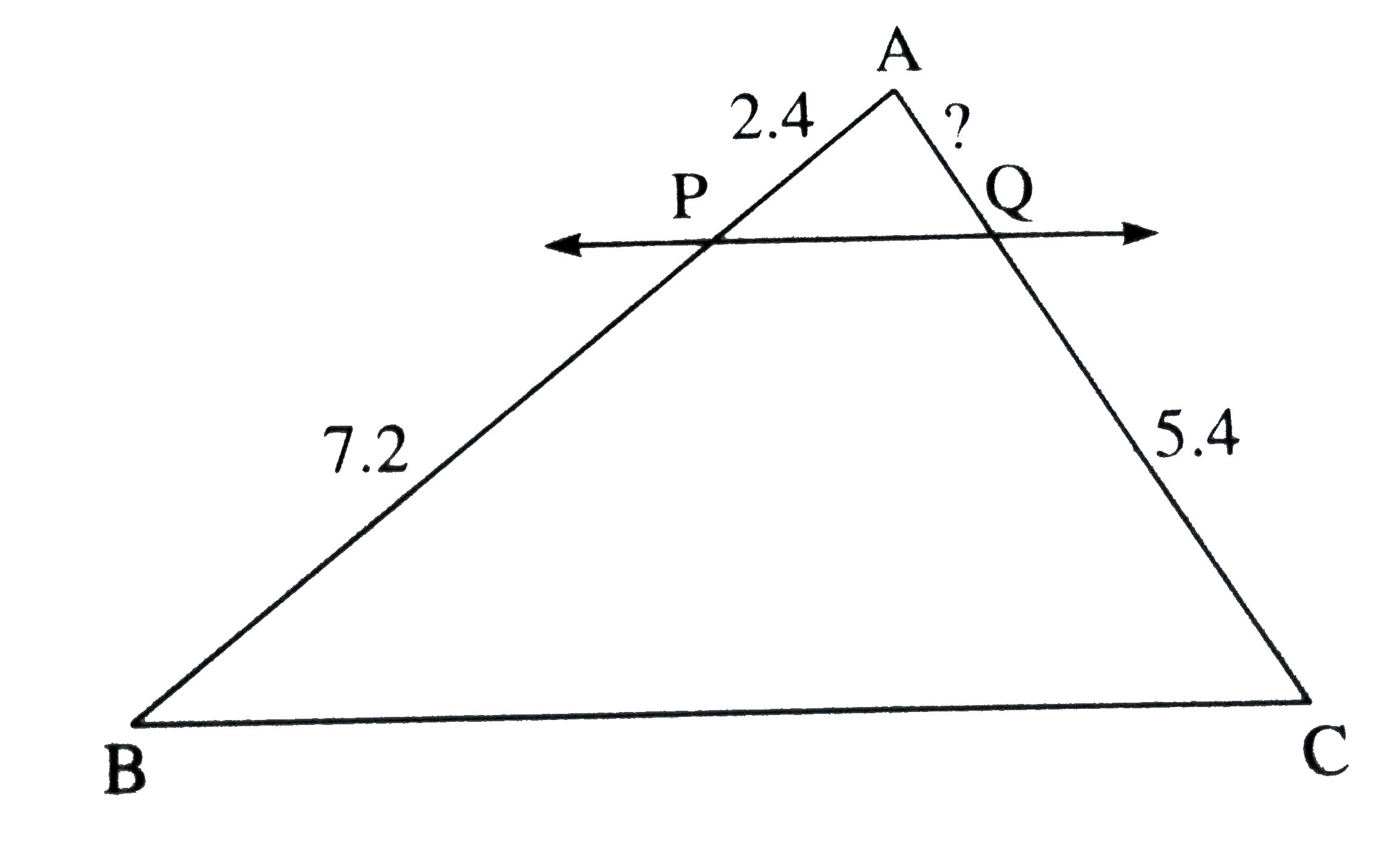
View SolutionIn the figure lien PQ∣∣ side BC,AP=2.4cm,PB=7.2cm,QC=5.4cm then find AQ.
View SolutionIf Q is a point on the side SR of a triangle PSR such that PQ=PR then prove that PS>PQ
View SolutionIn figure XY∣∣ seg AC. If 2AX=3BX and XY=9, complete the activity to find the value of AC.
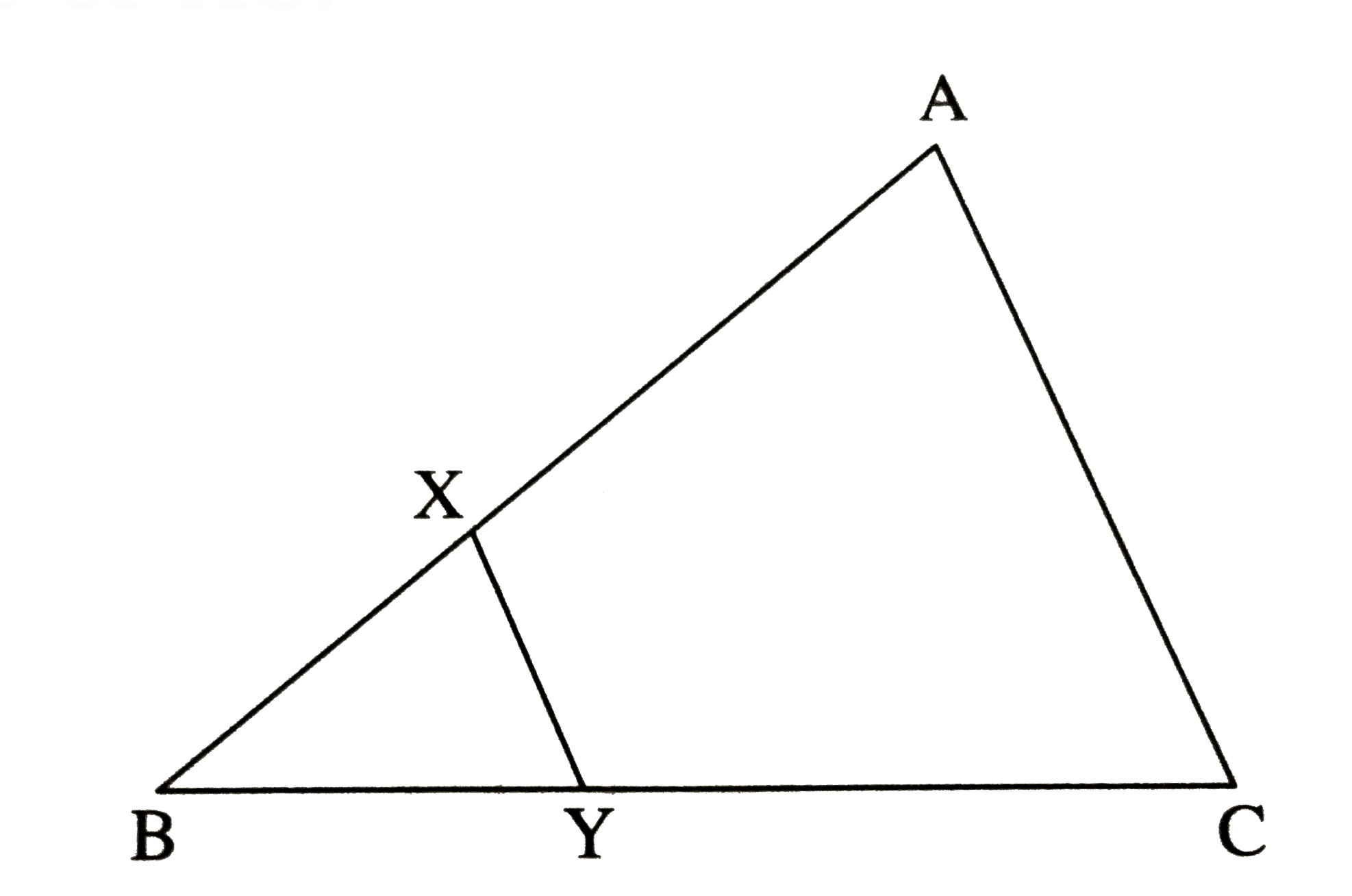
Activity: 2AX=3BX
∴AXBX=□□
∴AX+BXBX=□+□□.........(By componendo)
∴ABBX=□□.............1
ΔBCA~ΔBYX.......(□ test of similarity)
∴BABX=ACXY
..............(Corresponding sides of similar triangles)
∴□□=AC9
∴AC=□ ...........[From 1]
View SolutionName the types of following triangles :
Δ PQR such that PQ = QR = PR = 5 cm.
View SolutionΔPQR is an equilateral triangle. Seg PS⊥ side QR such that Q−S−R. Prove PS2=3QS2 by completing the following activity.
In ΔPQS,
∠PSQ=□……(Given)
∠Q=□………….(Angle of an equilateral triangle)
∴∠QPS=30∘.................(Remaining angle of ΔPQS)
∴ΔPQS is a □ triangle
PS=□PQ.............(Side opposite to 60∘)..............(1)
and QS=□PQ..........(Side opposite to 30∘)
PQ=2QS .....(2)
Substituting value of PQ from (2) in (1)
PS=√32×2QS
∴PS=□QS
∴PS2=3QS2......(Square both the sides)
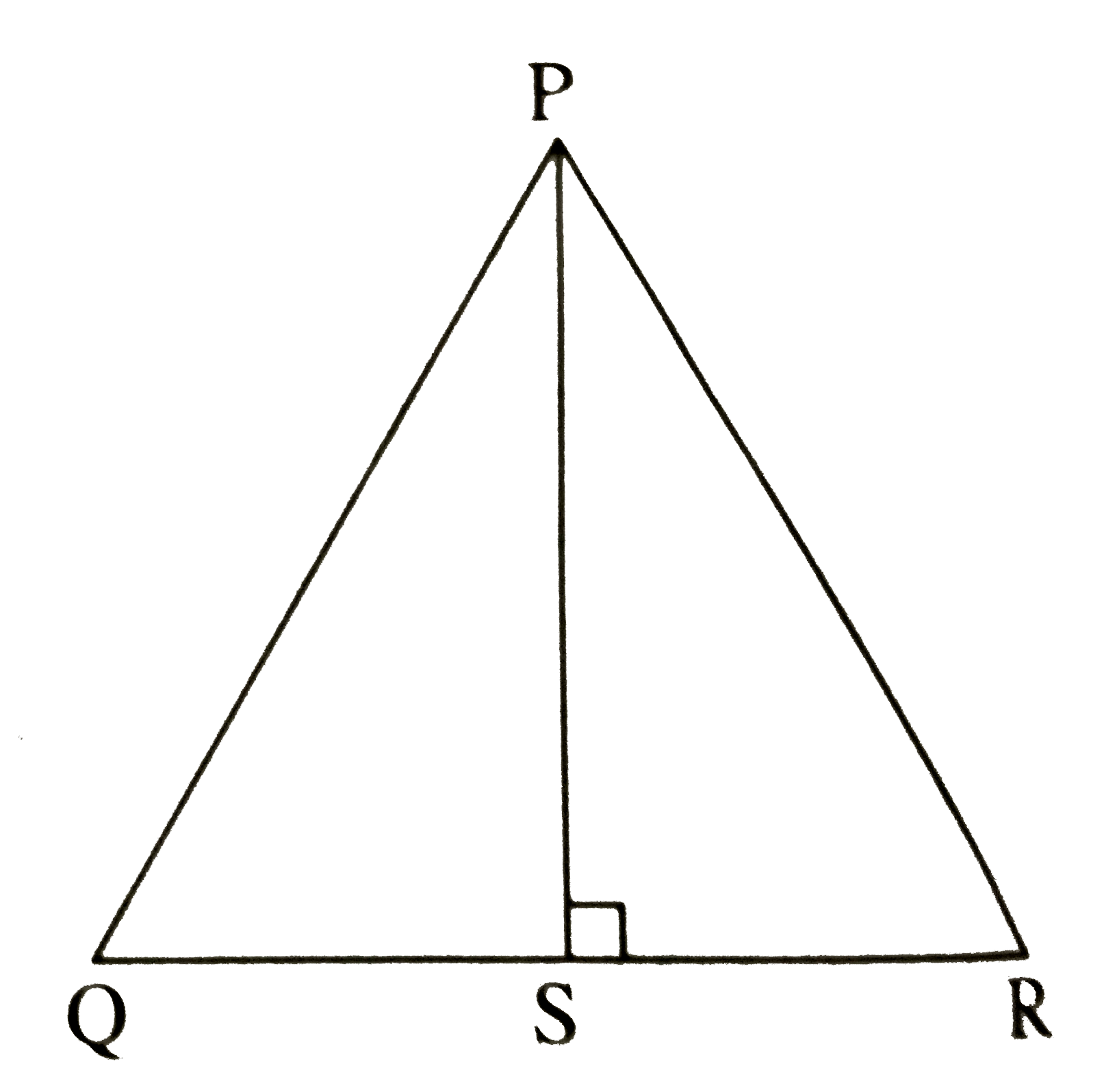
View SolutionConstruct a trapezium PQRs in which PQ∣∣SR,PQ=6.5cm,QR=4.5cm,PS=6cm and ∠Q=60∘.
View Solution
