L and M are the mid points of AB and BC respectively of ΔABC , right angled at B . 4LC2=

AB2+4BC2
BC2+4AB2
AC2+4AB2
None of these
The correct Answer is:A
Step by step video, text & image solution for L and M are the mid points of AB and BC respectively of DeltaABC , right angled at B . 4LC^(2)= by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Exercise (Multiple Choice Questions) (LEVEL -2)
15 Videos
- TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Exercise (Match the following )
3 Videos
- TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - NCERT Section Exercise 6 .6
12 Videos
- SURFACE AREAS AND VOLUMESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - OLYMPIAD/HOTS CORNER
20 Videos
Similar Questions
if D,E and F are the mid-points of the sides BC,CA and AB respectively of the ΔABCandO be any points, then prove that OA+OB+OC=OD+OE+OF
View SolutionIf (2, 1), (-1, -2), (3, -3) are the mid points of the sides BC, CA, AB respectively of ΔABC, then the equation of the perpendicular bisector of AB is ax+by+c=0, then (a+b+c) is _______.
View Solution
Knowledge Check
P and Q are the mid-points of the sides AB and BC, respectively, of ΔABC, right angled at B. Then:
AAQ2+CP2=AC2BAQ2+CP2=45AC2CAQ2+CP2=43AC2DAQ2+CP2=54AC2If ABC is a right angled triangle at B and M, N are the mid-points of AB and BC, then 4(AN2+CM2) is equal to :
A4AC2B5AC2C54AC2D6AC2In ΔABC,D and E are the mid points of sides BC and AC respectively. If AD=10.8 cm, BE =14.4 cm and AD and BE intersect at G at a right angle then the area (in cm2) of ΔABC is :
AA)103.68BB)56.76CC)80.64DD)53.76
In ΔABC , if L and M are the points on AB and AC, respectively such that LM∣∣BC. Prove that ar(ΔLOB)=ar(ΔMOC).
View SolutionIn the figure, ΔABC is right angled at B. If AB = 9 cm, AC = 15 cm. and D and E are the mid points of AB & AC respectively calculate.
(i) The length of BC
(ii) The area of trapezium BCED
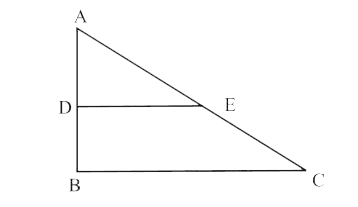
View SolutionIn the given Fig. 3, in ΔABC,DandE are the mid point of the sides AB and AC respectively. Find the length of DE. Prove that DE=12BC.
View SolutionThevertices of a triangle ABC are A(−7,8),B(5,2)andC(11,0). If D, E, F are the mid-points of the sides BC,CAandAB respectively, show that ΔABC=4ΔDEF.
View SolutionD is any point on side AC of ΔABC. If P,Q, X, Y are the mid points of AB,BC,ADandDCrespectively, then the ratio of PXandQYis
View Solution
