Let the vertex of an ∠ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half of the difference of the angles subtended by the chords AC and DE at the centre.
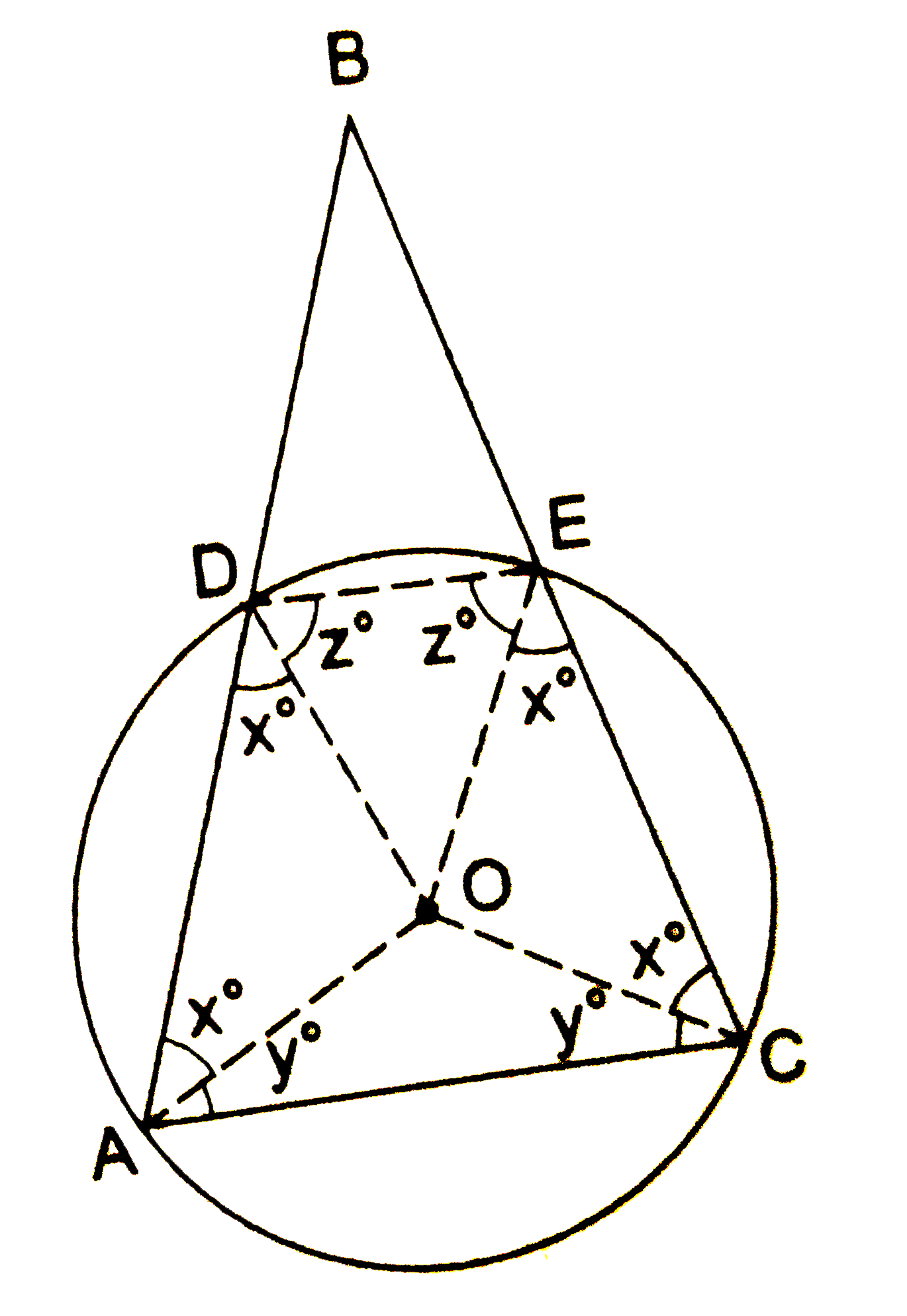
Let O be the centre of the given circle.
Let ADB and CEB be the two chords of the circle such that AD = CE.
Join OA,OC,OD,OE and DE.
Then , we have to prove that ∠ABC=12(∠AOC−∠DOE) .
In ΔOAD and ΔOCE, we have
OA = OC [radii of the same circle ]
OD = OE [radii of the same circle ]
AD = CE [given]
∴ΔOAD≅ΔOCE[ by SSS -congruence ].
So, ∠AOD=∠COE,OA=OC and OD = OE.
∴∠OAD=∠ODA=∠OCE=∠OCA=y∘ ( say )
∴∠AOC=(180∘−2y∘) . ...(i)
In ΔODE, we have
OD=OE⇒∠ODE=∠OED=z∘ ( say ).
∴∠ODE=(180∘−2z∘) ....(ii)
Clearly, ACED is a cyclic quadrilateral.
∴∠C+∠D=180∘⇒(x∘+y∘)+(x∘+z∘)=180∘
⇒2x∘+y∘+z∘=180∘ ....(iii)
Now, in ΔBDE, we have
∠BDE+∠BED+∠DBE=180∘
⇒[180∘−(x∘+z∘)]+[180∘−(x∘+z∘)]+∠DBE=180∘
⇒∠DBE=2x∘+2z∘−180∘
=180∘−(y∘+z∘)+2z∘−180∘ [using (iii) ]
⇒∠DBE=z∘−y∘
⇒∠ABC=z∘−y∘ .......(iv) [∵∠DBE=∠ABC]
From (i) and (ii) ,we get
(∠AOC−∠DOE)=(180∘−2y∘)−(180∘−2z∘)=2(z∘−y∘)
⇒12(∠AOC−∠DOE)=z∘−y∘ ....(v)
From (iv) and (v) , we have
12(∠AOC−∠DOE)=∠ABC
Topper's Solved these Questions
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Exercise 12A
22 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12B
18 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
Similar Questions
Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half of the difference of the angles subtended by the chords AC and DE at the center.
View SolutionLet the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre
View Solution
Knowledge Check
If the chord of a circle is equal to the radius of the circle, then the angle subtended by the chord at a point on the minor arc is:
A120∘B150∘C100∘D110∘
The chord of a circle is equal to its radius, find the angle subtended by this chord at the centre.
View SolutionProve that a diameter of a circle which bisects a chord of the circle also bisects the angle subtended by the chord at the centre of the circle.
View SolutionA chord of a circle is equal to the radius of the circle find the angle subtended by the chord at a point on the monor arc and also at a point on the major arc.
View SolutionIf the angles subtended by two chords of a circle at the centre are equal, the chords are equal.
View SolutionA chord of a circle is equal to its radius. The angle subtended by this chord at a point on the circumference is
View SolutionIf the angle subtended by two chords of a circle at the centre are equal; the chords are equal.
View SolutionTwo chords AB and AC of a circle are equal. Prove that the centre of the circle lies on the angle bisector of ∠BAC.
View Solution
