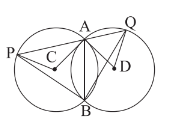
Like the adjoining figure, draw two circles with centres C and D which intersect each other at the points A and B . Draw a straight line through A which intersects the circle C at the point P and the circle with centre D at the point Q. Prove that (i) ∠PBQ=∠CAD(ii)∠BPC=∠BQD. Solution in Bengali
In the circle with centre C,the central angle produced by the chrod AP∠ACP and angle in circle = ∠ABP. By theorem-34,
∠ACP=2∠APBor,∠ABP=12∠ACP......(1)

Again, in the circle which centre at d, the central angle produced by the chord AQ=∠ADQ and angle in circle ∠ABQ.
∴ by theorem-34 ∠ADQ=2∠ABQor,∠ABQ=12∠ADQ.....(2)
then, adding (1) and (2) we get,
∠ABP+∠ABQ=12∠ACP+12∠ADQ
or, ∠PBQ=12∠ACP+∠ADQ
or, ∠PBQ=12(∠ACP+∠ADQ)
=12(180∘−2∠PAC+180∘−2∠QAD)
[∴∠ACP+∠PAC+∠PAC=180∘
or, ∠ACOP+∠PAC+∠PAC=180∘
or,ACP=180∘−2∠PAC
similiarly, ∠ADQ=180∘−2∠QAD]
or, ∠PBQ=12[360∘−2(∠PAC+∠QAD)]=12[360∘−2(180∘−∠CAD)]
=12[360∘−360∘+2∠ACD]=12×∠CAD=∠CAD
∴∠PBQ=∠CAD [ proved (i)]
Now, let us join B,C and B,D
∴CP=CB(∴ radii of same circle), ∴∠BPC=∠PBC......(3)
∴BD=DQ(∴ radii of same circle) ∴∠DBQ=∠DQB.......(4)
Now, from (i) we get,∠PBQ=∠CAD.
or,∠PBC+∠QBA=∠CAB+∠DAB
or,∠PBC+∠CBA+∠DAB
or, ∠PBC+∠CBA+∠DBA−∠DBQ=∠CAB+∠DAB
or, ∠PBC+∠CAB+∠DAB−∠DBQ=∠CAB+∠DAB
[∴CB=CA,∴∠CBA=CAB
∴DB=DA,∴∠DBA=∠DAB]
or, ∠PBC−∠DBQ=0or,∠PBCand∠DBQ=∠BQD]
∴∠BPC=∠BQD [ Proved (ii)]
Hence (i)∠PBQ=∠CADand(ii)∠BPC=∠BQD (Proved)
Topper's Solved these Questions
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXAMPLES (True or False)
4 Videos
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXAMPLES (Short-Answer Type Questions) MCQs
5 Videos
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXAMPLES (Short Answer Type Questions)
5 Videos
- THEOREMS RELATED TO CYCLIC QUADRILATERAL BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CYCLIC QUADRILATERAL EXERCISE - Long -answer type questions (L.A.)
12 Videos
- THEOREMS RELATED TO TANGENT IN A CIRCLE BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.2
23 Videos
Similar Questions
In the adjoining figure AD and BE are perpendicular ot BC and AC respectively of the ΔABC. The four points A,B,D,E are concylic.
View SolutionIn the adjoining figure, O is the centre of the circle AC is a diameter and chord DE is parallel to the diameter AC. If ∠CBD=60∘ , find the value of ∠CDE
View SolutionIn the adjacent figure O is the centre of the circle. If ∠OAB=30∘,∠ABC=120∘,∠BCO=y∘and∠COA=x∘, then the find value sof x and y.
View SolutionIn a cyclic quadrilateral, the ratio of three consecutive angle is 1 : 2 : 3 Find the value of first and third angles.
View SolutionThe distance of the point from the centre of a circle with diameter of 16 cm is 17 cm. Then the length of the tangent from the point to the circle is
View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect one circle at the points A and C and the other circle at B and D. Prove the AC|| BD
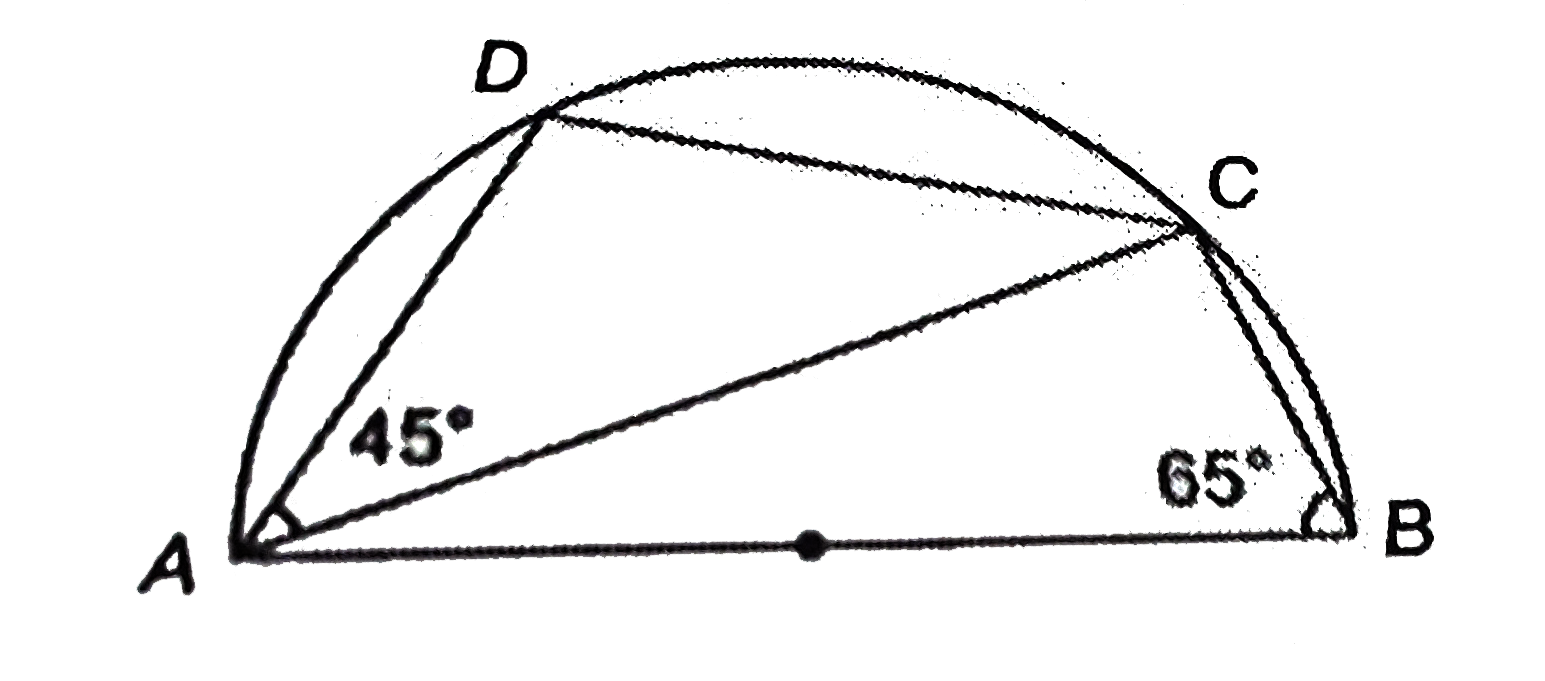
View SolutionIn the adjoining figure, AB is the diameter of the circle and two points C and D are on the circle. If ∠CAD=45∘ and ∠ABC=65∘, then find the value of ∠DCA.
View SolutionThe centre of two circle are P and Q they intersect at the points A and B. The straight line parallel to the line segment PQ through the point A intersects the two circles at the point C and D Prove that CD=2PQ
View SolutionTwo circles with centres A and B inrtersect each other at the points C and D. The centre B of the other circle lies on the circle with centre A. if ∠CQD=70∘, then find the value of ∠CPD.
View SolutionAnkita drew two circles which intersect each other at the points P and Q. Through the point P two straight lines are draw so that they intersect one of the circle at the points. A and B and the ohte circle at the points C and D respectively. Prove that ∠AQC=∠BQD.
View SolutionTwo chords AB and CD of the circle with centre at O intersect each other at an internal point P of the centre. Prove that ∠AOD+∠BOC=2∠BPC
View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect on circle at the points A and C and the other circle at B and D . Prove that AC||BD.
View SolutionIn two circles , one circle passes through the centre O of the other circle and they intersect each other at the points A and B . A straight line passing through A intersect the circle passing through O at the point P and the circle with centre at O at the point R . BY joining P , B and R , B prove that PR= PB.
View SolutionTwo chords AC and BD of a circle intersect each other at the point O. If two tangents drawn at the points A and B intersect each other at the point P and two tangents drawn at the points C and D intersect at the point Q, prove that ∠P+∠Q=2∠BOC.[GP−X]
View Solutionপাশের ছবির মতো C ও D কেন্দ্রবিশিষ্ট দুটি বৃত্ত অঙ্কন করেছি যারা পরস্পরকে A ও B বিন্দুতে ছেদ করেছে । A বিন্দুগামী একটি সরলরেখা অঙ্কন করেছি যা C কেন্দ্রীয় বৃত্তকে P বিন্দুতে এবং D কেন্দ্রীয় বৃত্তকে Q বিন্দুতে ছেদ করেছে । প্রমান করি যে, ∠PBQ=∠CAD
View Solution
