Question

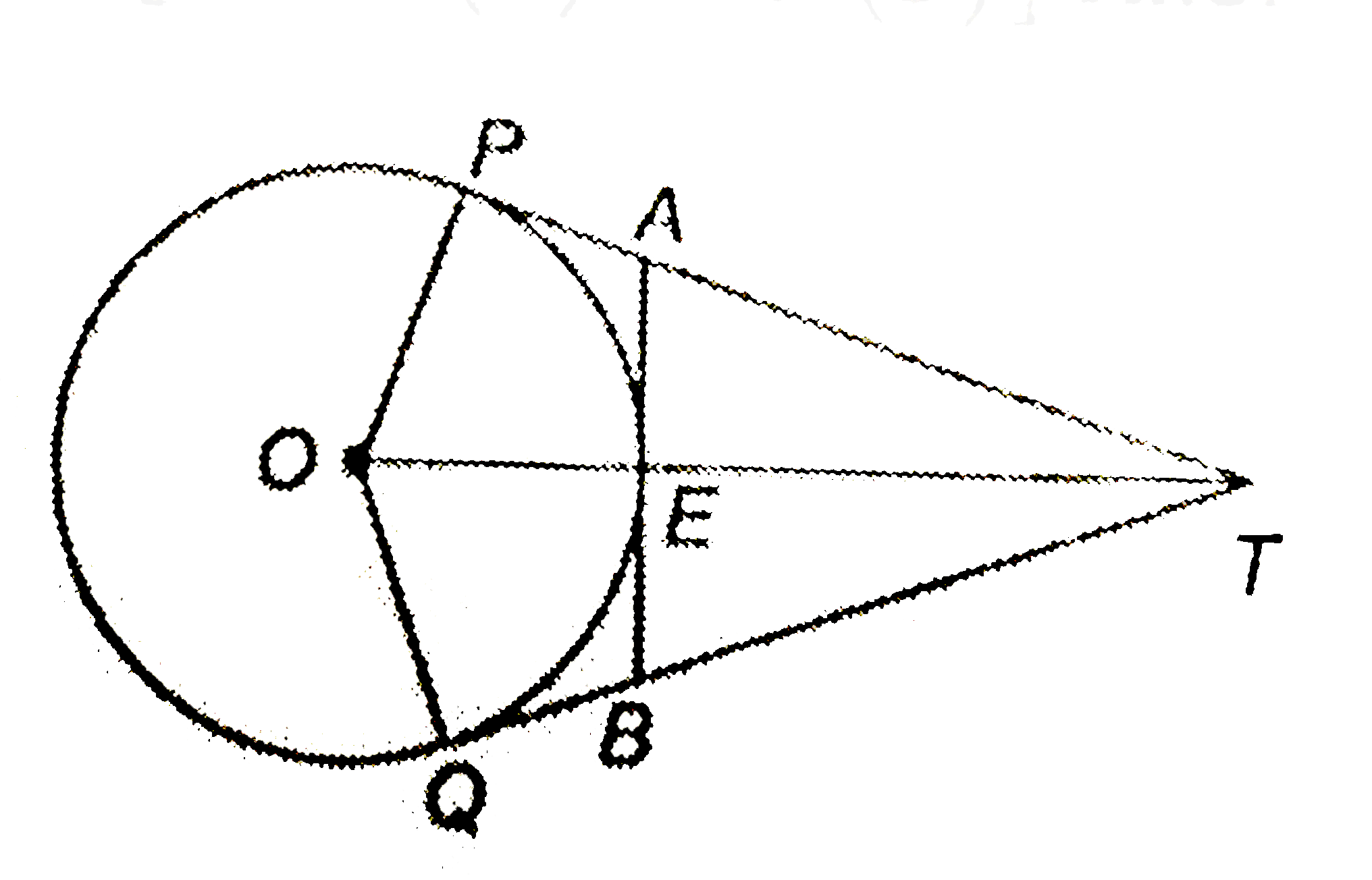
O

is the centre of a circle of radius

5cm.


T

is a point such that

OT=13cm and OT

intersects the circle at

E.

If

AB

is the tangent to the circle at

E,

find length of

AB.

Explanation

To find the length of the tangent $$AB$$ to the circle at point $$E$$, we can follow these steps:

Step 1: Identify the given information
- The center of the circle \( O \) has a radius of \( 5 \) cm.
- The distance from point \( O \) to point \( T \) is \( OT = 13 \) cm.
- The tangent \( AB \) touches the circle at point \( E \).

Step 2: Use the Pythagorean theorem
Since \( AB \) is a tangent to the circle at point \( E \), we can use the Pythagorean theorem in triangle \( OTE \):
\( OT^2 = OE^2 + ET^2 \)
Where:
- \( OT = 13 \) cm (distance from center to point T)
- \( OE = 5 \) cm (radius of the circle)
- \( ET \) is the length we need to find.

Substituting the known values:
\( 13^2 = 5^2 + ET^2 \)
\( 169 = 25 + ET^2 \)
\( ET^2 = 169 - 25 = 144 \)
\( ET = \sqrt{144} = 12 \text{ cm} \)

Step 3: Find the length of the tangent \( AB \)
The length of the tangent \( AB \) can be calculated using the property that the lengths of tangents drawn from an external point to a circle are equal. Let \( AP \) and \( BP \) be the lengths of the tangents from point \( T \) to points \( A \) and \( B \) respectively.

Since \( AP = BP \):
\( AB = AP + BP = 2 \times AP \)

From triangle \( OET \), we know that:
\( AP = ET = 12 \text{ cm} \)
Thus,
\( AB = 2 \times 12 = 24 \text{ cm} \)

Step 4: Conclusion
The length of the tangent \( AB \) is \( 24 \) cm.

---