P and Q are points on opposite sides AD and BC of a parallelogram ABCD such that PQ passes through the point of intersection O of its diagonals AC and BD. Show that PQ is bisected at O.
Given ABCD is a parallelogram whose diagonals bisect each other at O.
To show PQ is bisected at O.
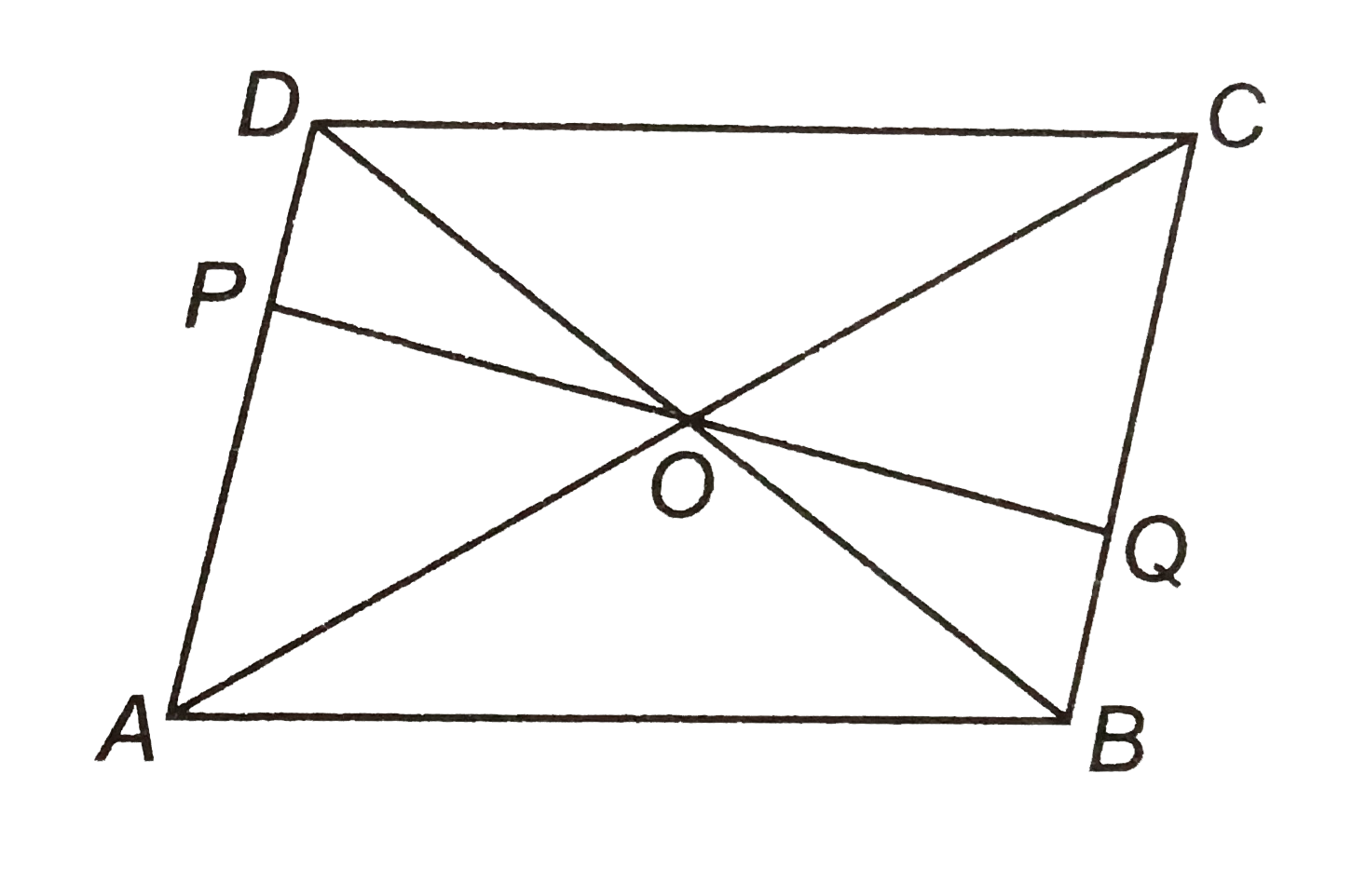
In ODP and OBQ,
[since, vertically opposite angles]
[alternate interior angles]
and
[by ASA congruence rule ]
[by CPCT rule]
So, PQ is bisected at O. Hence proved.
Topper's Solved these Questions
Similar Questions
M and N are points on opposite sides AD and BC of a parallelogram ABCD such that MN passes through the point of intersection O of its diagoinals AC and BD. Show that MN is bisected at O.
View SolutionABCD is a parallelogram and O is the point of intersection of its diagonals. If ar(△AOD)=4cm2 find ar(△AOB)
View Solution
Knowledge Check
P and Q are the points of trisection of the diagonal BD of a parallelogram ABCD. Then which of the following is true?
ACQ is parallel to APBCQ is perpendicular to APCCQ intersects APDNone of theseIn a parallelogram ABCD, a side AB is extended to E such that BE = AB. If DE cut the line BC at Q then point Q divide BC in what ratio?
A1:2B1:1C2:3D2:1
Points P and Q have been taken on opposite sides AB and CD, respectively of a parallelogram ABCD such that AP=CQ. Show that AC and PQ bisect each other.
View SolutionIn a parallelogram ABCD, points P and Q are points of trisection of diagonal BD. Prove that CQ is parallel to AP.
View SolutionThe diagonals of a parallelogram ABCD intersect at O.A line through O intersects AB at X and DC at Y. Prove that OX=OY.
View SolutionLet AD and BC be the parallel sides of a trapezium ABCD. Let P and Q be the midpoints of the diagonals AC and BD. If AD=16 and BC=20, what is the length of PQ?
View SolutionABCD is a parallelogram P is a point on AD suchAP.that APAD=12013. Q is the point of intersection of ACandBP. Calculate AQAC=
View SolutionIf the diagonals of a cyclic quadrilateral are perpendicular to each other, show that the line passing through the point of intersection of diagonals and midpoint of a side is perpendicular to the opposite side.
View Solution
