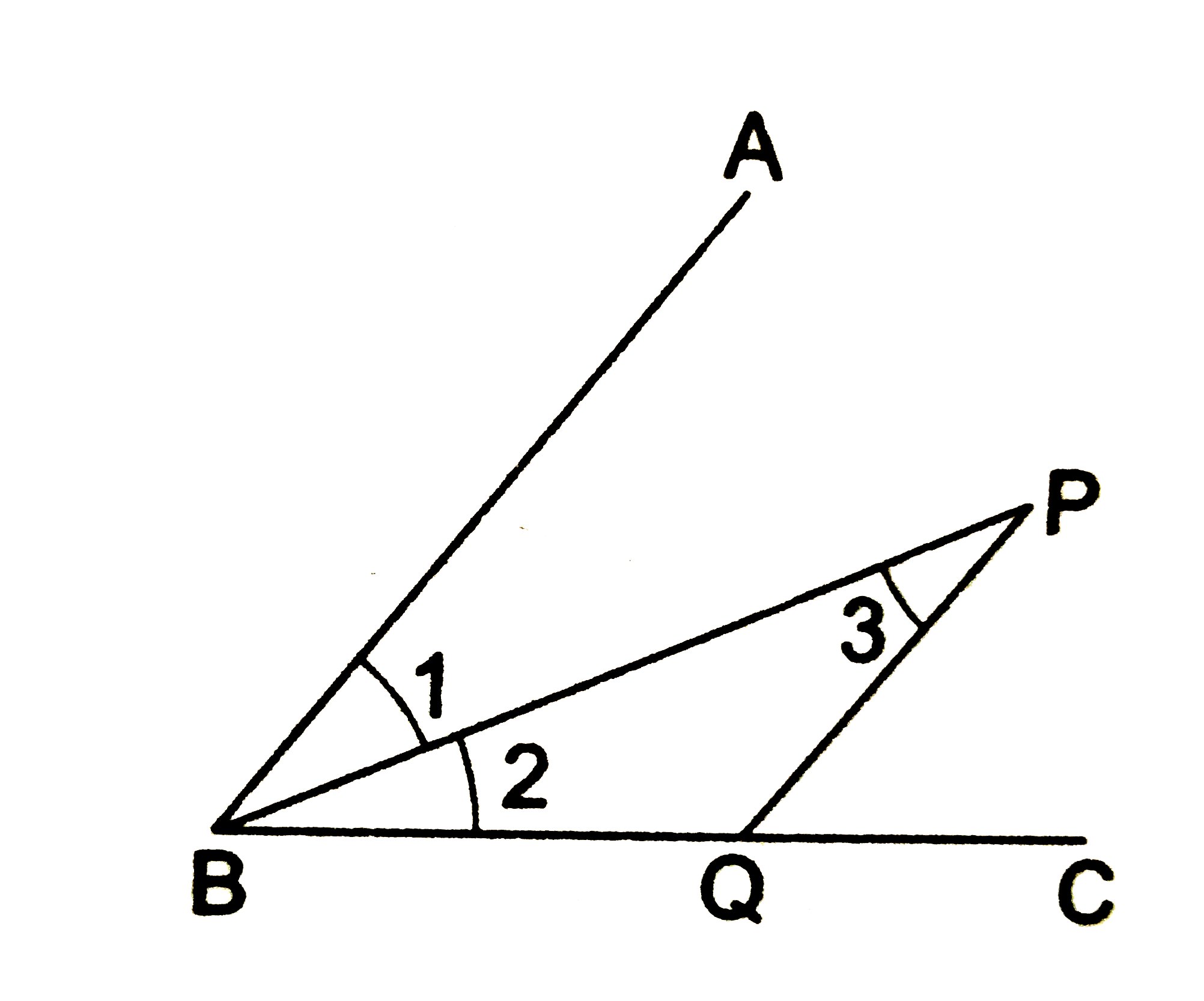
P is a point on the bisector of an angle ∠ABC. If the line through P parallel to AB meets BC at Q , prove that triangle BPQ is isosceles.
BA∣∣PQ and BP is transversal.
∴ ∠1=∠3⇒∠2=∠3 [∵∠1=∠2(given)].
∴ PQ=BQ.
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)
37 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)
22 Videos
Similar Questions
Knowledge Check
A triangle ABC is inscribed in a circle and the bisectors of the angles A, B and C meet the cir cumference at P, Q and R respec tively. The angles of the triangle PQR respectively are
A90∘−A2,90∘+A290∘+C2B90∘+A2,90∘−B2,90∘−CC90∘−A2,90∘−B2,90∘−C2DNone of these
In △ ABC, the bisectors of ∠B and ∠ C intersect at I. A line drawn through I and parallel to BC intersects AB at P and AC at Q. Prove that PQ = BP + CQ.
View SolutionP is the mid-point of side AB of a parallelogram ABCD . A line through B parallel to PD meets DC at Q and AD produced at R. Prove that: AR=2BC (ii) BR=2 BQ
View SolutionThe side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed as shown in Figure. Show that ar(^(gm)ABCD)=argmPBQR).
View SolutionThe side AB of a parallelogram ABCD is produced to any point P. A line through A parallel to CP meets CB produced in Q and the parallelogram PBQR completed. Show that ar(^(gm)ABCD)=ar(^(gm)BPRQ). CONSTRUCTION : Join AC and PQ. TO PROVE : ar(^(gm)ABCD)=ar(^(gm)BPRQ)
View SolutionAn exterior angle of a triangle is 1100 , and one of the interior opposite angles is 300. Find the other two angles of the triangle.
View SolutionTwo equal circles intersect in P and Q . A straight line through P meets the circles in A and B . Prove that QA=QB.
View SolutionP and Q are the points of trisection of the diagonal BD of a parallelogram ABCD. Prove that CQ is parallel to AP. Prove also that AC bisects PQ.
View Solution
