P is a point on the bisector of an angle ∠ABC. If the line through P parallel to AB meets BC at Q. prove that triangle BPQ is isosceles.Solution in Punjabi
Step by step video & image solution for P is a point on the bisector of an angle angleABC. If the line through P parallel to AB meets BC at Q. prove that triangle BPQ is isosceles. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
PQR is a triangle in which PQ=PR and S is any point on the side PQ. Through S, a line is drawn parallel to QR and intersecting PR at T. prove that PS=PT.
View SolutionFind the lateral surface and total surface area of a cuboid of length 80 cm, breadth 40 cm and height 20 cm.
View SolutionThe bisector of angleB of an isosceles triangle ABC with AB=AC meets the circumcircle of triangleABC at P as shown in the figure. If AP and BC produced meet at Q prove that CQ=CA.
View SolutionIn the given figure, in triangle ABC, D is the mid-point cf AB and P is any point on BC. If CQ || PD meets AB in Q and area of triangle ABC = 30 cm2, then, area of triangle BPQ is
View SolutionP is a point on the bisector of an angle ∠ABC. If the line through P parallel to AB meets BC at Q , prove that triangle BPQ is isosceles.
View SolutionP is a point on the bisector of ∠ABC .If the line through P,parallel to BA meet at Q ,prove that BPO is an isosceles triangle.
View Solutionबगल की आकृति ΔABC में ,D भुजा AB का मध्य बिंदु है| P ,BC पर कोई बिंदु है | CQ ,PD के समांतर ही तथा भुजा AB को Q पर प्रतिच्छेद करती है|
सिद्ध कीजिए की ar(ΔBPQ)=12ar(ΔABC)
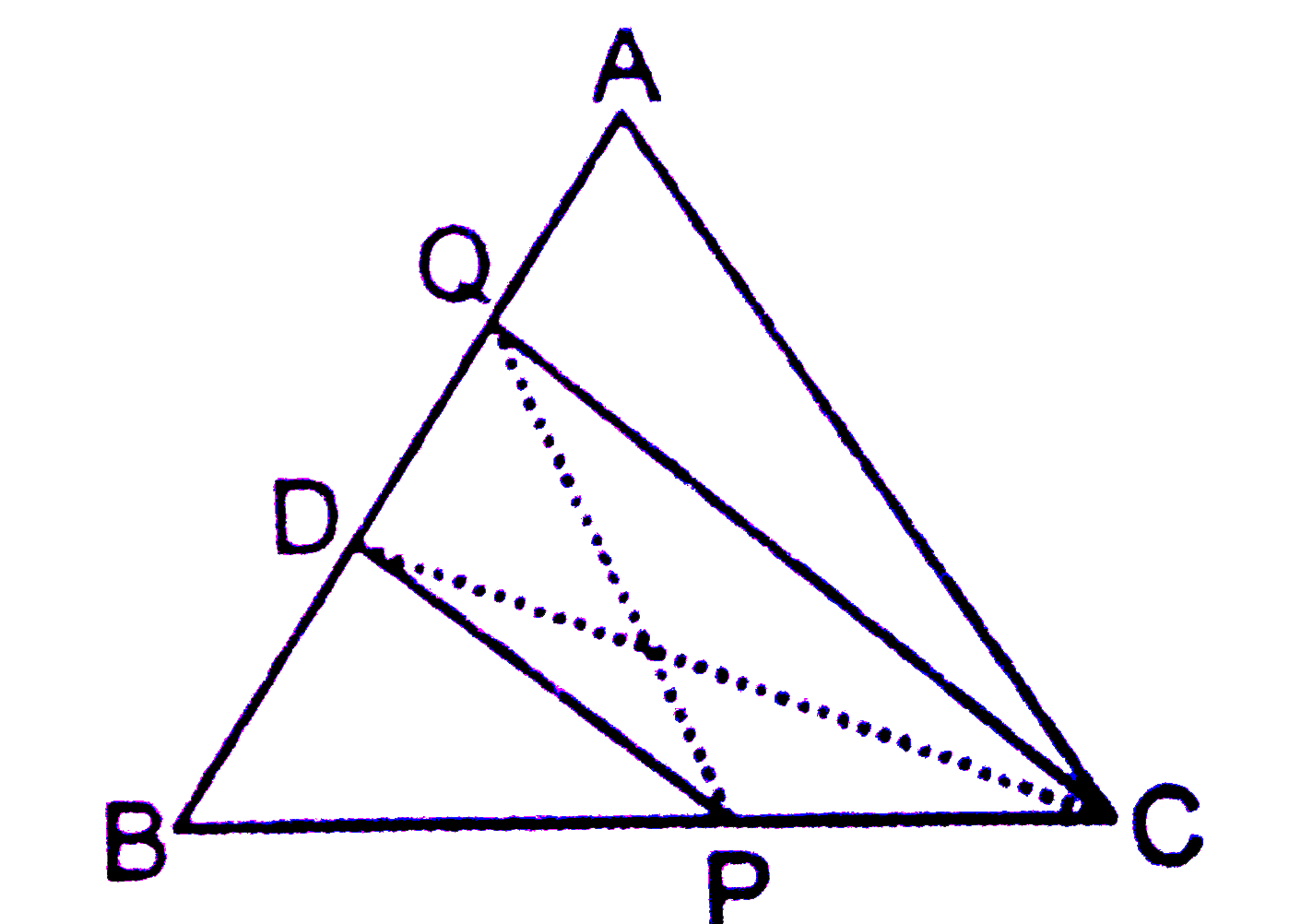
View Solutionकोण ∠ABCके समद्विभाजक पर स्थित एक बिन्दु P है | यदि P से AB से के समान्तर एक रेखा BC को Q पर काटती है, तो सिध्द करो कि PBQ त्रिभुज समद्विबाहु है |
View Solutionरेखा l, रेखांखण्ड BC का लंबसमद्विभाजक है। P, l पर कोई बिंदु है। सिद्ध करें कि PBC एक समद्विबाहु त्रिभुज होगा।
View SolutionP is a point on the bisector of ∠ABC .If the line through P, parallel to BA meet at Q ,prove that ΔBPQ is an isosceles triangle.
View SolutionP is a point on the bisector of an angle ∠ABC. If the line through P parallel to AB meets BC at Q , prove that triangle BPQ is isosceles.
View SolutionIn △ ABC, the bisectors of ∠B and ∠ C intersect at I. A line drawn through I and parallel to BC intersects AB at P and AC at Q. Prove that PQ = BP + CQ.
View SolutionIn △ ABC, the bisectors of ∠B and ∠ C intersect at I. A line drawn through I and parallel to BC intersects AB at P and AC at Q. Prove that PQ = BP + CQ.
View SolutionIn the parallelogram ABCD, the line drawn through Q point P on AB, parallel to BC meets AC at Q. The line through Q, parallel to AB meets AD R.
Prove that
APPB=ARRD.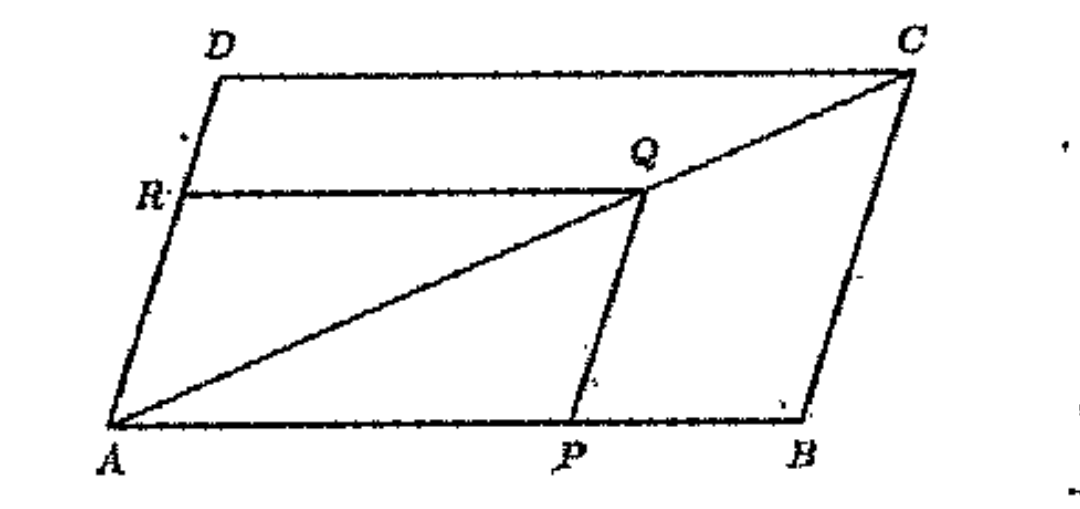 .
.
View SolutionIn triangle ABC, P is the mid-point of side BC. A line through P and parallel to CA meets AB at point Q and a line through Q and parallel to BC meets median AP at point R. Prove that :
AP=2AR
View SolutionIn triangle ABC, P is the mid-point of side BC. A line through P and parallel to CA meets AB at point Q and a line through Q and a line through Q and parallel to BC meets median AP at point R. Prove that :
BC=4QR.
View Solution
