P, Q , R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
To prove that the quadrilateral PQRS is a rhombus, we will follow these steps:
Step 1: Identify the midpoints
Let P, Q, R, and S be the midpoints of sides AB, BC, CD, and DA of quadrilateral ABCD respectively.
Step 2: Apply the Midpoint Theorem in triangles
1. In triangle ADC:
- S is the midpoint of AD and R is the midpoint of CD.
- By the Midpoint Theorem, we have:
- SR∥AC and SR=12AC (Equation 1)
2. In triangle ABC:
- P is the midpoint of AB and Q is the midpoint of BC.
- By the Midpoint Theorem, we have:
- PQ∥AC and PQ=12AC (Equation 2)
Step 3: Compare segments SR and PQ
From Equation 1 and Equation 2, we can conclude:
- Since both SR and PQ are equal to 12AC, we have:
- SR=PQ
Step 4: Apply the Midpoint Theorem in triangles BCD and ABD
1. In triangle BCD:
- R is the midpoint of BC and Q is the midpoint of CD.
- By the Midpoint Theorem, we have:
- RQ∥BD and RQ=12BD (Equation 3)
2. In triangle ABD:
- P is the midpoint of AB and S is the midpoint of AD.
- By the Midpoint Theorem, we have:
- PS∥BD and PS=12BD (Equation 4)
Step 5: Compare segments RQ and PS
From Equation 3 and Equation 4, we can conclude:
- Since both RQ and PS are equal to 12BD, we have:
- RQ=PS
Step 6: Use the given condition
Given that AC=BD, we can now summarize:
- From previous steps:
- SR=PQ (both equal to 12AC)
- RQ=PS (both equal to 12BD)
- Since AC=BD, we have:
- SR=PQ=RQ=PS
Conclusion
Since all four sides of quadrilateral PQRS are equal, we conclude that PQRS is a rhombus.
---
Let P, Q, R, and S be the midpoints of sides AB, BC, CD, and DA of quadrilateral ABCD respectively.
1. In triangle ADC:
- S is the midpoint of AD and R is the midpoint of CD.
- By the Midpoint Theorem, we have:
- SR∥AC and SR=12AC (Equation 1)
- P is the midpoint of AB and Q is the midpoint of BC.
- By the Midpoint Theorem, we have:
- PQ∥AC and PQ=12AC (Equation 2)
From Equation 1 and Equation 2, we can conclude:
- Since both SR and PQ are equal to 12AC, we have:
- SR=PQ
1. In triangle BCD:
- R is the midpoint of BC and Q is the midpoint of CD.
- By the Midpoint Theorem, we have:
- RQ∥BD and RQ=12BD (Equation 3)
- P is the midpoint of AB and S is the midpoint of AD.
- By the Midpoint Theorem, we have:
- PS∥BD and PS=12BD (Equation 4)
From Equation 3 and Equation 4, we can conclude:
- Since both RQ and PS are equal to 12BD, we have:
- RQ=PS
Given that AC=BD, we can now summarize:
- From previous steps:
- SR=PQ (both equal to 12AC)
- RQ=PS (both equal to 12BD)
- Since AC=BD, we have:
- SR=PQ=RQ=PS
Since all four sides of quadrilateral PQRS are equal, we conclude that PQRS is a rhombus.
Topper's Solved these Questions
- QUADRILATERALS BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - QUADRILATERALS EXERCISE - SHORT ANSWER TYPE QUESTIONS
10 Videos
- POLYNOMIALSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - POLYNOMIALSEXERCISE - EXERCISE 2.4 Long Answer type Questions
9 Videos
- STATISTICS AND PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - LONG ANSWER TYPE QUESTIONS
12 Videos
Similar Questions
P, Q, R and S are respectively the mid-points of sides AB, BC, CD and DA of quadrilateral ABCD in which AC=BD and AC⊥BD. Prove that PQRS is a square.
View SolutionABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View SolutionIf the sides of a quadrilateral ABCD touch a circle prove that
AB+CD=BC+AD.
View SolutionABCD is a rhombus and P, Q, R and S are wthe mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
View SolutionThe given figure shows a quadrilateral ABCD in which E, F, G and H are the midpoints of consecutive sides of ABCD. Again P, Q, R and S are the mid-points of the consecutive sides of quadrilateral EFGH. If EFGH is a rectangle, show that : PQRS is a rhombus.
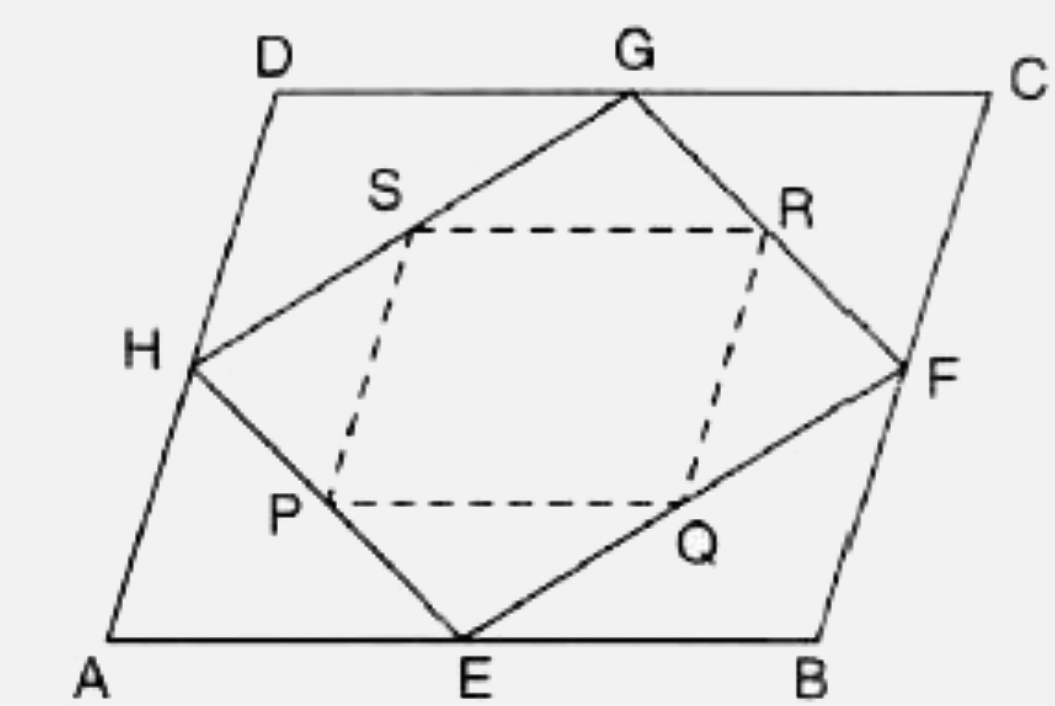
View SolutionABCD is a quadrilateral. Is AB+BC+CD+DA>AC+BD?
View SolutionP,Q,R and S are the mid points of sides AB,BC , CD and DA respectively of rhombus ABCD. Show that PQRS is a rectangle.
Under what conditions will PQRS be a square ?
View SolutionABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA. AC is a diagonal. Show that : (i) SR ∣∣ AC and SR=12AC (ii) PQ=SR (iii) PQRS is a parallelogram
View SolutionABCD is a rectangle formed by the points A(1, 1),B(1, 4),C(5, 4) and D(5, 1). P, Q, R and S are the midpoints of AB, BC, CD and DA respectively. Is the quadrilateral PQRS a square? A rectangle? or a rhombus? Justify your answer.
View SolutionP and Q are the mid-point of the opposite sides AB and CD of a parallelogram ABCD. AQ intersects DP at S and BQ intersects CP at R. Show that PQRS is a parallelogram.

View Solution
