PA and PB are tangents to a circle S touching it at points A and B. C is a point on S in between A and B as shown in the figure. LCM is a tangent to S intersecting PA and PB in S at points L and M, respectively. Then the perimeter of the triangle PLM depends on o
A,B,C and P
P but not on C
P and C only
the radius of S only
The correct Answer is:B
Perimeter of ΔPLM=PL+LC+CM+MP
PL+LA+BM+MP
=PA+PB.
Topper's Solved these Questions
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - JEE Advanced (Single Correct Answer Type)
14 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Question Bank
30 Videos
Similar Questions
PA and PB are tangents to a circle S touching it at points A and B. C is a point on S in between A and B as shown in the figure. LCM is a tangent to S intersecting PA and PB in S at points L and M, respectively. Then the perimeter of the triangle PLM depends on o
View SolutionFrom an external point P, tangents PA and PB are drawn to a circle. CE is a tangent to the circle at D which intersect PA and PB at point E and C respectvely. If AP=15 cm, find the permeter of the △PEC.
View Solution
Knowledge Check
PA and PB are tangents to a circle with centre O, from a point P outside the circle and A and B are points on the circle. If ∠APB=30∘, then ∠OAB is equal to :
AA) 40∘BB) 15∘CC) 50∘DD) 25∘PA and PB are tangents to a circle with centre 0, from a point P outside the circle, and A and B are point on the circle. If ∠APB=30∘, then ∠OAB is equal to:
A25∘B40∘C15∘D50∘
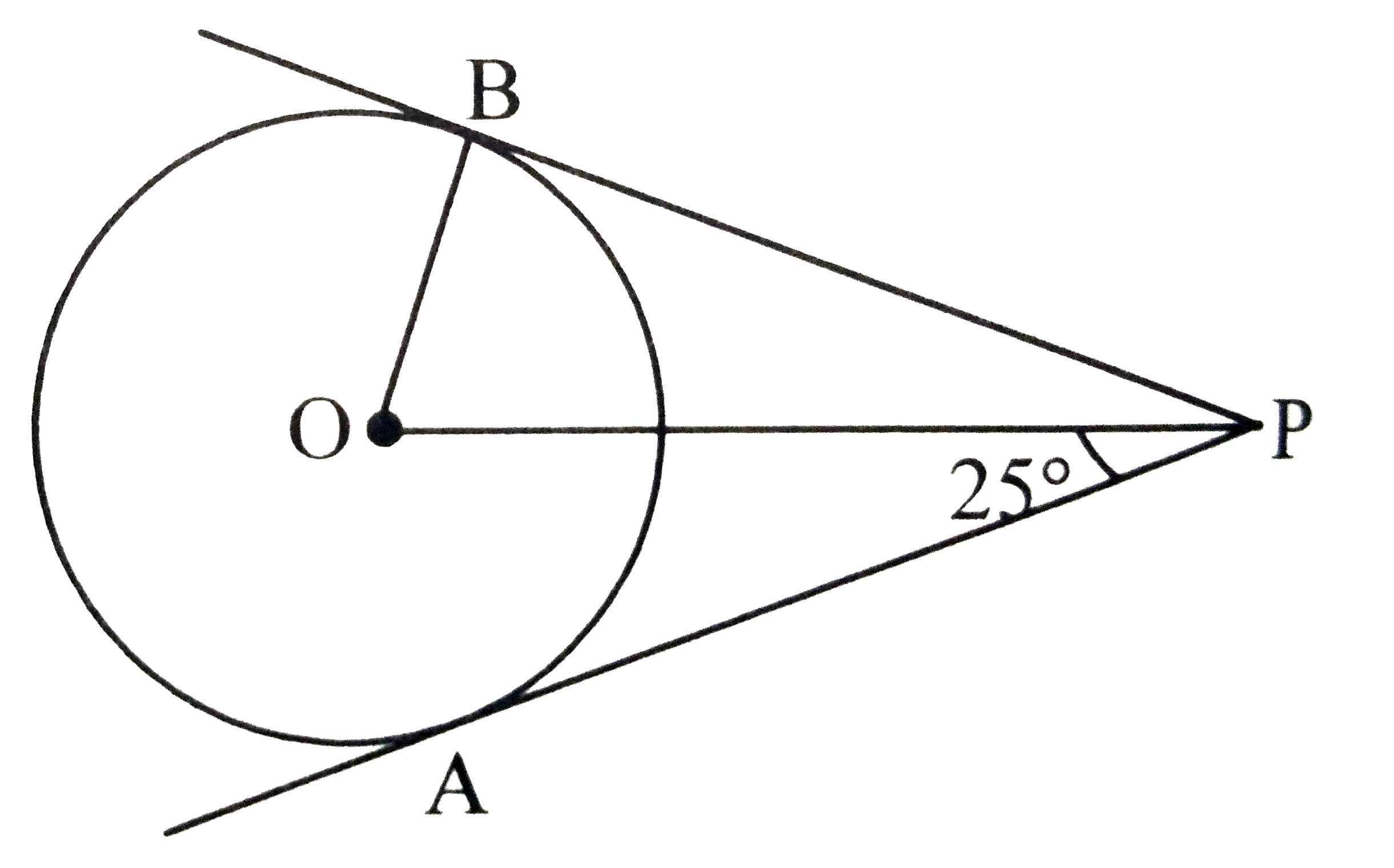
PA and PB are tangents to the circle with centre O touching it at A and B respectively. IF ∠APO=25∘ , then ∠POB is
View SolutionFrom an external point P, two tangents, PA and PB are drawn to a circle with centre 0. At one point E on the circle tangent is drawn which intersects PA and PB at C and D, respectively. If PA=10 cm, find the perimeter of the triangle PCD.
View SolutionAs shown in the figure, PA is a tangent to a circle and PBC is a secant, so that PB = AB. Prove that PB.PC=AC2
View Solution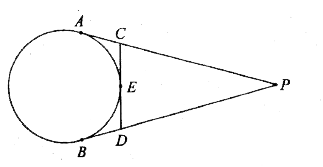
From an external point P tangents PA and PB are drawn to the circle as shown in the above figure. CD is the tangent to the circle at E. If AP 16 cm, then the perimeter of the triangle PCD is equal to
View SolutionPA and PB are tangents to a circle with centre O from point P. OP is equal to the diameter of the circle. Prove that ABP is equilateral triangle,
View SolutionLine L is tangent to unit circle S at point P .Point A and the circle S are on the same side of L and the distance from A to L is 3 units.Two tangents from point A intersect line L at point B and C then the value of PB.PC is equal to
View Solution
