Prove that , "If a line parallel to a side of a triangle intersects the remaining sides in two distinct points then the line divides the sides in the same proportion".
Proof : ΔXAB and ΔBAY have a common vertex B and their bases XA and AY lie on the same line XY.
∴ they have equal heights.
∴A(ΔXAB)A(ΔBAY)=XAAY …[Triangles of equal heights ] ….(1)
ΔXAB and ΔABZ have a common verte A and their bases XB and BZ lie on the same line XZ.
∴ they have equal heights.
∴A(ΔXAB)A(ΔABZ)=XBBZ ....[Triangles of equal heights] ....(2)
∴ΔBAY and ΔABZ lie between the same two parallel lines AB and YZ.
∴ they have equal heights, also have same base AB.
∴A(ΔBAY)=A(ΔABZ).... [Triangles of equal bases and heights ] ....(3)
∴ from (1) , (2) and (3) , we get
A(ΔXAB)A(ΔBAY)=A(ΔXAB)A(ΔABZ) ....(4)
∴ from (1) ,(2) and (4) , we get
XAAY=XBBZ
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - THEOREMS EXERCISE - PYTHAGORAS THEOREM4videos
THEOREMS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - THEOREMS EXERCISE - CIRCLE15videos
THEOREMS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - STATISTICSEXERCISE - EXAMPLES FOR PRACTICE (MCQs)35videos
STATISTICS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIGONOMETRYEXERCISE - CHALLENGING QUESTIONS6videos
TRIGONOMETRY
Similar Questions
(B) Solve any two of the following subquestions :
Prove that following statement, " If a line parallel to a side of a Delta intersects the remaining sides in two distinct points , then the line divides the sides in the same proportion . "View SolutionProve that, if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
Using the above result, do the following:
In Fig. 7 .45 DE||BC and BD = CE. Prove that ΔABC is an isosceles triangle.
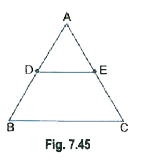 View Solution
View SolutionProve that if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then the other two sides are divided in the same ratio.
View SolutionTheorem 6.1 : If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
View SolutionIf a line is drawn to one side of a triangle to intersect the other two sides in distinct points, prove that the other two sides are divided in the same ratio.
View SolutionBasic proportionality Theorem or Thales Theorem - If a line is drawn parallel to one side of a triangle intersecting the other two sides; then it divides the two sides in the same ratio.
View SolutionIf a line is drawn parallel to one side of a triangle to intersect the other two sides in disinct points, the other two sides are divided in the same ratio. Using this theoure. Find EC in if DE∣∣BC.
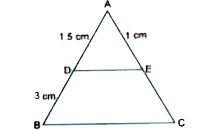 View Solution
View SolutionProve that a line drawn from the vertex of a triangle to its base is bisected by the line joining the mid points of the remaining two sides of the triangle.
View SolutionIf a line through one vertex of a triangle divides the opposite sides in the Ratio of other two sides; then the line bisects the angle at the vertex.
View SolutionTheorem 6.2 : If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
View Solution

